Это цитата сообщения галина_соловьева Оригинальное сообщение
Детский час. Мистер Самоделкин - 2013/12.
 [480x700]
[480x700]Это цитата сообщения astro-2012 Оригинальное сообщение
Каким для вас будет год Лошади?

Каким для вас будет год Лошади?
Интересное:
 |
 |
| Собака, дерево и веревка | В лучах утреннего солнца |
Это цитата сообщения галина_соловьева Оригинальное сообщение
Тарабарина. Оригами и развитие ребенка.
Популярное пособие для родителей и педпгогов.
 [472x700]
[472x700]Это цитата сообщения ЛИДАНА Оригинальное сообщение
Интересные сайты для обработки фото..
Интересные сайты для обработки фото..
|
Это цитата сообщения Julia_Ljuva Оригинальное сообщение
Мастерим из бумажных тарелочек















Это цитата сообщения LediLana Оригинальное сообщение
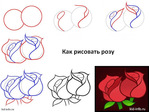
21 вариант как рисовать розу
Это цитата сообщения LediLana Оригинальное сообщение
Плетение из фольги – модный современный вид рукоделия
Цветок из фольги с МК
Готовый цветок трудно было сфотографировать хорошо, потому что фольга даёт сильные блики, но всё равно видно, какой он получается красивый!
1.
Это цитата сообщения beautyB Оригинальное сообщение
Создание слайд-шоу из фотографий...
|
Это цитата сообщения alona777 Оригинальное сообщение
Радужное Дерево. МК. от Loretta Grayson.
Это цитата сообщения fljuida Оригинальное сообщение
Декорируем при помощи фольги.
Фольга для декора.
Благодаря фольге и всевозможным дополнительным рельефным изделиям можно получить оригинальную поверхность, которой оформляются не только панно , но и поверхности на предметах декора интерьера.
 [показать]
[показать]
А вот как это сделать, Вы узнаете чуть ниже :) Пока рассмотрите варианты :) Надеюсь они Вас зажгут на творчество :)
Это цитата сообщения fljuida Оригинальное сообщение
Декор фольгой.
Способ декорирования фольгой.
Фольга является прекрасным материалом для декора предметов и я не раз уже выставляла посты, в которых показывала всевозможные способы декора с применением этого чудесного доступного всем материала :) На этой страничке мы рассмотрим вариант использования в качестве подложки под фольгу горячий клей, которым можно отлично повторять контур любого рисунка. Наложенная сверху фольга с последующим патинированием даже обувным кремом - прекрасная имитация кованки :) А в конце странички я выложила некоторые красивые трафареты , чтобы все у Вас сразу было под рукой :)
Это цитата сообщения галина_соловьева Оригинальное сообщение
Голубь. Итоговое тестирование - 4 класс. Математика, русский язык.
Тесты - удобная форма итогового усвоения программного материалы по русскому языку и математике в начальной школе. Тестовые задания - экономия времени урока и удобная форма проверки с минимальной подготовкой со стороны учителя. Одной из целью данного сборника является быстрая проверка знаний учащихся, окончивших 4 класс, по русскому языку и математике. Пособие предназначено учителям и учащимся начальных классов, может быть полезно родителям для проверки уровня готовности детей к тестированию. 2012г.
 [494x700]
[494x700]Это цитата сообщения КолыбельнаяМедведицы Оригинальное сообщение
Рисунки клеем и солью
-нарисуйте рисунок с помощью клея пва
-засыпьте контур солью
-переверните лист бумаги,чтобы удалить лишнюю соль
-с помощью мокрой кисти наносим акварель на соленый контур
Источник http://vk.com/club2756772
1.
 [595x564]
[595x564] 2.
 [452x604]
[452x604] 3.
 [480x604]
[480x604] 4.
 [573x604]
[573x604] 5.
 [604x401]
[604x401] 6.
 [466x530]
[466x530] 7.
 [530x436]
[530x436]
Это цитата сообщения Мираж_ок Оригинальное сообщение
Теория множественного интеллекта
Теория множественного интеллекта — теория, предложенная Говардом Гарднером в 1983 году как модель интеллекта, которая рассматривает интеллект в различных конкретных (в первую очередь сенсорных) условиях, а не как доминирование одной общей способности к чему-либо.
Гарднер утверждает, что существует широкий спектр когнитивных способностей и есть лишь очень слабая корреляция между ними. Например, теория предсказывает, что ребёнок, который легко обучается умножению, не обязательно, как правило, более умный, чем ребёнок, который имеет большие трудности в обучении этому процессу.
Ребёнок, который тратит больше времени, чтобы освоить простое умножение:
1) может лучше научиться умножению через другой подход;
2) может преуспеть в поле за пределами математики;
3) возможно, даже смотрит на понимание процесса умножения на принципиально более глубоком уровне или, возможно, как на совершенно другой процесс.
Такое принципиально более глубокое понимание может привести к тому, что внешне выглядит как медлительность, но на самом деле может скрыть математический интеллект потенциально выше, чем у ребёнка, который быстро запоминает таблицу умножения, несмотря на менее глубокое понимание процесса умножения как такового.
Это цитата сообщения СЕМЬЯ_И_ДЕТИ Оригинальное сообщение
Как мы воспитываем своих детей? Скрытые послания
 Каждый день мы каким-либо образом общаемся со своими детьми. Как правило, у каждого родителя есть некий набор фраз, шаблонов или привычных и устойчивых словосочетаний, с помощью которых он, родитель, пытается воспитывать своего ребенка. Эти наши привычные повседневные фразы содержат особую информацию, невидимые на первый взгляд скрытые послания.
Каждый день мы каким-либо образом общаемся со своими детьми. Как правило, у каждого родителя есть некий набор фраз, шаблонов или привычных и устойчивых словосочетаний, с помощью которых он, родитель, пытается воспитывать своего ребенка. Эти наши привычные повседневные фразы содержат особую информацию, невидимые на первый взгляд скрытые послания.На основе именно таких скрытых родительских посланий и утверждений ребенок составляет мнение о самом себе, о людях, об окружающем его мире. Мы специально составили данную подборку из различных источников, позаимствовав материалы у различных авторов, чтобы каждый родитель (или ребенок) мог наглядно увидеть, к чему могут привести некоторые формы воспитания и общения.