Ну, что же, друзья... Мы с вами поговорили о белых карликах, нейтронных звездах, гравитационных волннах, темной материи и темной энергии. Пришла пора поговорить о самых распиаренных среди домохозяек астрономических объектах - о Черных дырах ( далее - ЧД)

Но сначала 

Ликбез

Немного математики. Без нее никак. Начнем с школьной, закончим университетской.

Кто не знает теоремы Пифагора? Любая домохозяйка в курсе, что «Пифагоровы штаны на все стороны равны» или, выражаясь научным языком, квадрат гипотенузы равен сумме квадратов катетов

С² = А² + В²

Давайте положим, что А=Х, В=Y.

Примем, что X– горизонтальная ось координат, абсцисса, Y– вертикальная ось координат, ордината. Координатная сетка у нас, естественно, декартова, т.е. прямоугольная. И не двумерная, а трехмерная. Мы же в трехмерном пространстве живем.

Пусть точка А имеет координаты X_a, Y_a, Z_aточка В имеет координаты X_b, Y_b, Z_b.

Тогда длина отрезка, соединяющего точки А и В как раз из теоремы Пифагора и определяется:

L² = (X_a - X_b)² + (Y_a - Y_b)² + (Z_a – Z_b)²

Теперь от школьной математики плавно переходим к высшей. Обозначим оси координат не X, Y, Z, а X¹, X², X³, или, обобщенно, Xⁱ, где индекс i пробегает значения от 1 до 3-х. Почему? А патамушта, высшие математики не ограничиваются тремя измерениями, а работают сразу с общим случаем, где измерений N, причем N может быть равно чему угодно, в том числе и бесконечности, а букв английского алфавита всего 24)).

А почему индекс вверху, там, где обычно ставится показатель степени?

А патамушта. Так принято в дифференциальной геометрии, а ею мы сейчас и займемся.

Вернемся к нашим точкам. Обозначим их координаты для А как X_aⁱ, для В как X_bⁱ, и положим, что

X_bⁱ= X_aⁱ+ dXⁱ

где dXⁱ– бесконечно малое приращение соответствующей координаты, дифференциал, по научному. Отсюда и дифференциальная геометрия.

Тогда длина бесконечно малого перемещения из точки А в любую бесконечно близкую точку пространства будет равна

(dS)² = (dX¹)² + (dX²)² + (dX³)²                                                                       (1)

Примечание1: везде в левых частях уравнений стоит не длина, а квадрат длины, чтобы не заморачиваться в правых частях с квадратными корнями)

Примечание 2: почему приращение не конечное, а бесконечно малое? Представим, что нам надо померять длину окружности, а линейка у нас длиной с ее диаметр? Получится? Совсем не получится. А если длина линейки равна радиусу? Получится, но результат выйдет очень неточным. А если длина линейки = 1/100 радиуса? Вот тут мы получим результат измерения, который будет отличаться от истинной длины на сотые процента. В этом и заключен смысл понятия дифференциал. Суммируя бесконечно малые отрезки мы получаем истинную длину кривой. Правда, и слагаемых у нас получается бесконечно много. Такая операция суммирования как называется? Интегрирование. Все это придумали Ньютон и Лейбниц, за что им большое человеческое спасибо.. 

Так. Все понятно? Неплохо продвигаемся. Теперь мы совершаем переход от институтского к университетскому уровню.  Перепишем выражение (1) в виде

(dS)² = g₁₁dX¹ dX¹ + g₁₂dX¹ dX² + g₁₃dX¹ dX³ + g₂₁dX² dX¹+ … + g₃₃dX³dX³                               (2)

Нетрудно (а кому трудно, надо поднапрячься) видеть, что таких слагаемых у нас будет девять. Вопрос, каким должен быть коэффициент g_ij, где i, j пробегают значения от 1 до 3, чтобы выражения (1) и (2) были тождественны? Я люблю задавать вопросы на сообразительность, но здесь мучить своих читателей не буду.  Если человек не знаком с математикой, и может на него ответить, то это живой Гаусс или даже Гильберт, а вероятность встречи с таковым персонажем равна нулю. ИБО. Человек с настолько феноменальными математическими способностями не математиком быть не может. Так что, сразу ответ.

g_ij= 1, если i= j

g_ij= 0, если i не равно j

Прикол? Да, вот такой математический трюк. Между прочим, подобный g_ij называется «символом Кронекера», научная штука, а не какой-нибудь курьез.

Зачем он нужен? Давайте выпишем компоненты g_ijв виде таблицы

|g₁₁g₁₂g₁₃|    |1 0 0|  
|g₂₁g₂₂g₂₃|  =|0 1 0|                                                                                     (3)
|g₃₁g₃₂g₃₃|    |0 0 1|

Такая таблица называется «матрицей», в нашем случае порядка 3 х3

Но у нее есть еще одно название: «метрический тензор».

Ура. Мы добрались до Общей теории относительности и Эйнштейна. Ну а уж если мы добрались до Эйнштейна давайте перепишем выражение для квадрата длины бесконечно малого перемещения, а в ОТО оно называется «интервалом», в эйнштейновском виде:

(dS)² = g_ijdXⁱdX^j                                                                                               (4)

Длинную сумму из 9 слагаемых мы записали в компактном виде, в котором по совпадающим нижним-верхним индексам предполагается суммирование. Это называется «правилом суммирования Эйнштейна».

Для чего это нужно? 

Смысл выражения (4), а по-научному, оно называется «квадратичной формой», в том, что это не что иное, как обобщенная теорема Пифагора, позволяющая вычислять расстояния между точками по их координатам. А метрический тензор – правило, по которому вычисляются расстояния.

В Евклидовом, то есть трехмерном, плоском пространстве он тождественен символу Кронекера, т.е. состоит из нулей и единиц. Физический смысл этого факта в том, что в любой точке Евклидова пространства расстояния вычисляются одинаковым образом.

Ситуация меняется вблизи массивных тел. В гравитационном поле компоненты метрического тензора начинают зависеть от координат. Это самое главное, фундаментальное следствие ОТО – в присутствии источника гравитации в каждой точке пространства свое правило измерения расстояний.

Найти эту зависимость можно, решив уравнение Эйнштейна:

                                                             (5)

(индексы тут греческие, мю и ню, но это сути наших рассуждений не меняет)

R_μν– тензор Римана - мера кривизны (неевклидовости)) пространства, он представляет собой хитрую комбинацию, составленную из метрического тензора. Т_μν - тензор энергии-импульса, характеристика гравитирующего объекта. Задав тензор энергии-импульса, и  решив уравнение (5), мы найдем зависимость метрического тензора g_μν от координат. Собственно, это и будет конечным результатом, который мы хотим получить. Имея метрический тензор, мы можем полностью описать свойства пространства вокруг центра гравитации и движение объектов в его поле.

Метрика Шварцшильда

Первым уравнение Эйнштейна решил… сам Эйнштейн. Но решил он его приближенно, что дало ему возможность качественно предсказать некоторые следствия своей теории, но о количественных характеристиках речь тогда не шла. Но, то, что, вблизи массивного объекта метрика пространства искажается, расстояния как бы растягиваются, было ясно уже  из приближенного решения. Откуда сразу же выводятся главные эффекты ОТО: замедление времени и гравитационное красное смещение. Почему? Скорость света. Он постоянна во всех системах отсчета и не зависит от координат. А что такое время? Это, формально, расстояние, деленное на скорость. Расстояния увеличиваются, скорость постоянна.  Следовательно? Вот то-то и оно))... 

...Однако, менее чем через год после публикации ОТО, Карл Шварцшильд нашел точное (аналитическое) решение уравнений Эйнштейна для случая идеально-сферического не вращающегося тела. Вскоре после этого Шварцшильд умер, ему было всего 42 года. Колоссальная потеря для науки.

Анализ решения Шварцшильда показывает, что оно имеет две особенности: при r=0, и при r=r_s компоненты метрического тензора обращаются в бесконечность. Такие особенности решений называются сингулярностями. Физически, это означает, что в центре масс источника гравитации и на сфере радиуса r_s от него расстояния между близкими точками обращаются в бесконечность. А бесконечное расстояние означает и бесконечное время процесса. 

Надо ли говорить о том, что решение Шварцшильда и есть предсказание существования такого объекта, как Черная дыра, а r_s– сейчас называют радиусом Шварцшильда или  «горизонтом событий». На радиусе Шварцшильда вторая космическая скорость для гравитирующего тела становится равной скорости света, отсюда, любая материя или излучение, провалившееся за горизонт, никогда из-под него не выйдут. Среди домохозяек это считается главным свойством ЧД.

Но мы не домохозяйки,  и руководствуемся математикой, а не лирикой.  А с точки зрения математики у решения Шварцшильда есть куда более интересная особенность: две сингулярности оно имеет в системе отсчета, связанной с удаленным наблюдателем, то есть с Евклидовым (плоским) пространством. Если же связать систему отсчета с телом, движущимся в гравитационном поле, то сингулярность при r=r_s устраняется, т.е. эта сингулярность относительна. Сингулярность при r=0 выбором системы координат устранить не удается. Эта сингулярность абсолютна.

Какой в этом физический смысл?

Допустим, около ЧД звездной массы, но в нескольких миллионах (десятках миллионов) километров от нее, там, где пространство (почти) Евклидово, летает космический корабль с двумя космонавтами (астронавтами). Допустим, что один из них, назовем его Гагариным, вывалился из корабля, а второй, назовем его Армстронгом, остался.  

Гагарин падает в ЧД, а на его скафандре «победной молнией пульсирует фонарь». Ну, а что? Гагарин имеет перспективу стать первым человеком, ступившим на радиус Щварцшильда, потому-то он и Гагарин. Это ли не победа? Русские же везде первые, везде побеждают.  Пусть фонарь у него пульсирует с частотой 1 раз в секунду и пульсирует белым светом.

Что увидит Армстронг? Он связан с системой отчета Евклидова пространства, для него существуют две сингулярности, поэтому, он сначала будет видеть, как Гагарин постепенно ускоряется в направлении ЧД, частота пульсаций и цвет фонаря при этом не изменится. Но при подлете к r_s Армстронг обнаружит, что фонарь Гагарина пульсирует все реже, а цвет фонаря меняетcя с белого, через желтый и оранжевый, на красный, потом на темно красный, потом свет, вообще, исчезнет, а период пульсаций растянется на миллиарды лет. Иначе говоря, Армстронг не увидит, как Гагарин пересек горизонт. Да даже если бы он и мог видеть Гагарина, он бы, все равно, триумфа российской космонавтики не дождался. С точки зрения Армстронга Гагарину нужно бесконечное время для пересечения горизонта.

А что Гагарин? Он связан с локальной неинерциальной (ускоренной) системой координат, относительно которой он покоится. Для него сингулярности при r=r_s не существует, он пересечет горизонт за конечное собственное время и даже этого не заметит. Почему? А патамушта, раз для него решение Шварцшильда имеет единственную сингулярность при r=0, то все остальные точки пространства для Гагарина, что вблизи Армстронга, откуда он начал свой высокий полет, что вблизи горизонта, одинаковы.  

Правда, не все так радужно для русскага космонавта. Горизонт он пересечет за конечное время, а вот в центральную сингулярность будет падать бесконечно долго даже по собственным (локальным) часам. Ну и, само собой, провалившись за горизонт, выбраться из-под него, и доложить о свершении  Сами-Знаете-Кому он уже не сможет.

Однако, нарисованная нами картина покорения горизонта русским космонавтом идеализирована. Если речь идет о ЧД звездной массы, то за горизонт провалится не Гагарин, а элементарные частицы, который когда-то были Гагариным. На  них русскага космонавта разорвут приливные силы.

Откуда они берутся? ЧД звездной массы – чрезвычайно компактный, даже точечной объект по астрономическим меркам. ЧД массы Солнца имеет радиус всего 3 км, а радиус Солнца полтора миллиона километров. И вблизи такого компактного объекта метрика начинает меняться стремительно на считанных метрах дистанции.  Получиться  что на макушке Гагарина расстояния существенно меньше расстояний у его пяток. Звучит бредово, но в пространстве с настолько быстро меняющейся метрикой, Гагарин, чьи органы зрения назодятся на голове станет сторонним наблюдателем для своих пяток. То есть, как единый объект он перестанет существовать. В философском смысле. Да и в физическом тоже: вблизи горизонта Гагарин увидит, как его ноги по неведомой для него причине отрываются от туловища, а голова от плеч. Потом, при подлете непосредственно к Горизонту, по той же причине, все, что осталось от Гагарина будет разорвано на молекулы, молекулы на атомы, атомы на элементарные частицы, а они - на кварки.

Что будет дальше - непонятно. Вообще, состояние материи внутри Горизонта и в сингулярности вопрос дискуссионный и чрезвычайно темный. Сколько-нибудь внятных теорий на этот счет нет. 

Метрика Керра

Решение Шварцшильда описывает самую простую из всех возможных задач - сферически-симметричный случай. Соответственно, решается задача в сферических координатах. 

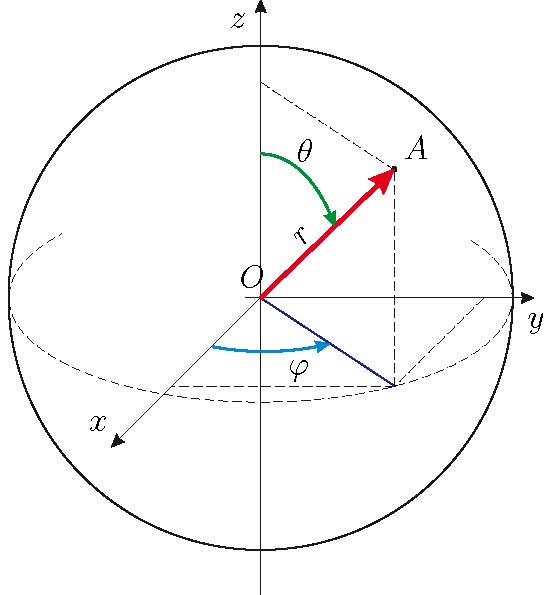
Самое обычное дело. Мы такими координатами постоянно пользуемся. θ — это широта, φ - долгота, а третья координата, r, нам, живущим на поверхности Земли без надобности.

В решении Шварцшильда без надобности как раз широта и долгота. Все свойства решения, в силу сферической симметрии зависят только от радиуса. Иначе говоря, в процессе решения можно смело положить производные по широте и долготе равными нулю.

Но метрика Шварцшильда описывает нереалистичный случай. В Космосе все объекты вращаются. И вращение драматически усложняют задачу. Почему? Геометрию вращающегося тела нельзя считать сферически симметричной. В ней есть выделенное направление — ось вращения, а в сферической симметрии все направления равноправны. Задача о вращающемся теле осесимметрична, и производная по широте уже не нулевая. Отсюда и повышенная сложность задачи. Ее решения пришлось ждать почти 50 лет, до 1961 года, когда Рой Керр опубликовал результаты своих исследование вращающегося сферического тела.

Метрика Керра сильно отличается от метрики Шварцшильда, математические выражения для компонентов метрического тензора тут безумно сложные. Но, главное в том, что компонент тензора, соответствующий долготе зависит не только от пространственных координат, но и от времени. Физический смысл такового математического факта означает, что кроме сферы Шварцшильда вокруг вращающегося тела возникает еще одна особая область — эргосфера.

Ее поверхность еще называют пределом статичности (static limit). Смысл его в том, что любое тело, попавшее под предел статичности получает ускорение по долготе. Это следствие зависимости компонента, отвечающего за долготу, от времени. Иначе говоря, вращающаяся ЧД создает вокруг себя «водоворот» пространства, который подхватывает любую материю, будь то вещество или излучение. Это подобно тому, как мы размешиваем чай ложечкой. От размешивания чаинки, свободно весящие в жидкости, увлекаются ее потоком, собираются на оси вращения и оседают на дно. Очень похоже на процессы, идущие вокруг ЧД Керра.

Но это еще далеко не все. Обратим внимание на рисунок. Во-первых, сингулярность уже не точка, как в ЧД Шварцшильда, а кольцо, диаметр которого зависит от момента импульса ЧД, т.е., от ее массы и скорости вращения.

Во-вторых у ЧД Керра есть два горизонта событий — внешний (outer) и внутренний (inner). Что это такое?

Допустим, Армстронг и Гагарин из предыдущего примера, взявшись за руки, падают в ЧД Керра. Когда они пересекут эргосферу, они обнаружат, что по непонятной причине они начали вращаться вокруг некоего центра вращения. Каким они его видят — вопрос открытый до сих пор. Горизонтов они, как и в предыдущем случае не видят, их видят только сторонние наблюдатели, но есть существенное отличие. Внешний горизонт космо-астро-навты пересекут за конечное время для себя и бесконечное для стороннего наблюдателя. Если они так и продолжат падать в сцепке, то провалятся за внутренний горизонт и навсегда сгинут в сингулярности. Но, если, внезапно, до пересечения внутреннего горизонта Гагарин решит пожертвовать собой (он же советский человек!), и оттолкнет от себя Армстронга, то Гагарин провалится под внутренний горизонт, а Армстронг, счастливый и довольный, вылетит из-под внешнего горизонта, да еще и со скоростью, большей, чем он туда влетал. ЧД при этом немного притормозит. Совсем чуть-чуть. По-научному, если тело провалилось под внешний горизонт, его можно выбить оттуда, приложив к нему некую стороннюю силу. Например, сбросить часть массы или включить реактивные двигатели (что тоже самое, что и сброс массы).

Правда радуется Армстронг рано. С точки зрения сторонних наблюдателей, то есть всей нашей Вселенной, он падал на внешний горизонт бесконечное время. Как же он может вылететь из-под него? В какой момент времени? Ответ прост: никак. Никак в нашей Вселенной. Армстронг вылетит в какую-то другую, параллельную Вселенную.

Звучит фантастически. В прямом смысле, ведь параллельные миры - одна из магистральных тем современной НФ. Оказывается, это отнюдь не фантастика, а чистая математика. Мало того, ЧД Керра математически обосновывает и второй основной сюжет НФ — машину времени.

Во всех предыдущих рассуждениях я не упоминал, что пространство ОТО отнюдь не Евклидово. Исправляюсь. В ОТО все вычисления производятся в пространстве Минковского, метрический тензор которого уже не матрица 3х3, а 4х4. К трем координатам X¹, X², X³ добавляется четвертая X⁰=Ct. И точка в этом 4-пространстве в проекции на наше привычное трехмерное - это точка в 3-пространстве и момент во времени. Соответственно, то, что мы называем траекториями или орбитами в 3-пространстве, в пространстве Минковского имеют совершенно иной вид и называются «мировыми линиями». Так вот, математика нам говорит, что между эргосферой и внешним горизонтом ЧД Керра возможно существование замкнутых мировых линий. То есть мировая линия, начавшись и некоей точке 4-пространства делает петлю и возвращается в нее же. То есть в ту же точку 3-пространства и в тот же момент времени. В прошлое, иначе говоря.

Ничего себе.

Наконец, из метрики Керра следует, что существуют некое пороговое значение момента импульса гравитирующего тела при превышении которого сингулярность образуется, а вот горизонты событий вокруг нее — нет. Это случай так называемой «голой» (nacked) сингулярности. То есть, внешние наблюдатели могут ее видеть. Ситуация нормальная для математиков, но совершенно невообразимая для физиков.

И вот такие математические выверты, в которых трудно найти физический смысл, а, зачастую и прямо противоречащие оному — это не слишком хорошо для ОТО. Да, она с высокой точностью описывает многие природные феномены, но и вводит в научный обиход феномены фантастические. Что это? Несовершенство ОТО, которая в случае ЧД выходит за границы своей применимости? Или несовершенство нашего разума, который все еще и во многом обывательский?

Время покажет.

Да, ну а что же практика, которая критерий истины?

Практика

Как искать ЧД звездной массы? Как обнаружить объект, который взаимодействует с окружающим миром только через гравитацию, да еще и точечный по сути?

В случае одиночной ЧД — никак. Искать Черные дыры надо в тесных двойных звездных системах. Если нам удастся найти звезду, которая ведет себя как двойная, т.е. колеблется вокруг некоего центра, но второй компонент никакими наблюдениями не обнаруживается, это может быть шанс на черную дыру. Если при этом мы увидим, что нечто стягивает с такой звезды вещество и закручивает его в аккреционный диск, а в центре диска пустота, шансы на обнаружение ЧД значительно вырастут. Если же при этом, окажется, что невидимый компонент по массе превосходит предел масс для нейтронной звезды, шансы вырастут многократно.

Сейчас имеются данные о, по крайней мере, двух объектах, которые могут оказаться черными дырами с высокой степенью вероятности. Это Лебедь Х-1 и V616 Единорога. Их свойства: наличие аккреционного диска, джетов, мощность рентгеновского излучения от диска и масса невидимой компоненты точно соответствуют свойствам ЧД.

Но, помимо ЧД звездных масс существуют и сверхмассивные Черные дыры (СМЧД), массой от миллионов до миллиардов солнечных масс. Как они образовались - вопрос дискуссионный, но все ядра спиральных галактик сегодня считаются таковыми. И это, по-видимому, самое лучшее доказательство существования ЧД как явления природы.

Почему лучшее?  Самая близкая к нам СМЧД - ядро нашей собственной Галактики, объект Стрелец А*. Он лежит от нас в 30 тысячах световых лет, и в оптическом диапазоне не наблюдается - его скрывают плотные газо-пылевые облака, которые сосредоточены в плоскости галактического диска.

Зато он виден в радиодиапазоне. Источник окружают облака сильно ионизированного газа, они то и излучают радиоволны. Анализ движения облаков и отдельных звезд, вращающихся вокруг Стрельца А* показывает, что его линейный размер не больше 44 млн. км., фактически, это диметр орбиты Меркурия, а масса 4.3 миллиона солнечных масс. Радиус Шварцшильда для такой массы - 12 млн. км. Что это может быть, роме ЧД? Никакого другого объяснения природы объекта с такой экстремальной плотностью и размером не предложено. 

Так что, старик Эйнштейн прав и на этот раз. Один из столпов науки, Нильс Бор, по-моему, назвал Общую теорию относительности наиболее совершенным творением человеческого разума.  Чем больше узнаешь эту теорию, тем уверенней понимаешь, что это так и есть. Беда, правда, в том, что она, теория, очень плохо визуализуется в каких-то бытовых образах, которыми человек и мыслит. Намного хуже квантовой теории. Это чистая математика, абстракция, но, эта абстракция и качественно, и количественно объясняет всю совокупность гравитационных эффектов. По крайней мере, всю известную совокупность. 

Так, может, и фантастические чудеса, которые следуют из ОТО - кротовые норы, параллельные миры, машина времени, все это тоже есть в реальности? Или за пределами ОТО есть другая, более фундаментальная теория, свободная от фантастичности, в которую ОТО входит как некий предельный случай? 

Как знать, как знать...