Лабиринтами – (от греч. Λαβιριγοξ – labyrinthos) в древней Греции и Египте –  большое здание, дворец со множеством комнат и запутанными переходами (Толковый словарь Ушакова). Авторы античности называли лабиринтами сооружения со множеством коридоров, комнат, перекрестков и тупиков, из которых было трудно найти выход. А первое извсестное упоминание о лабиринте – это микенская глиняная табличка, обнаруженная в Кноссе (около 1400 г. до н.э.). Возможно, слово «лабиринт» связано со словом «лабрис», двусторонний топор, символизирующий два рога священного быка. Поклонение этому быку было частью минойской (критской) религии, находившейся под сильным влиянием мифологии. Однако, и сегодня этимология этого слова до конца не ясна.

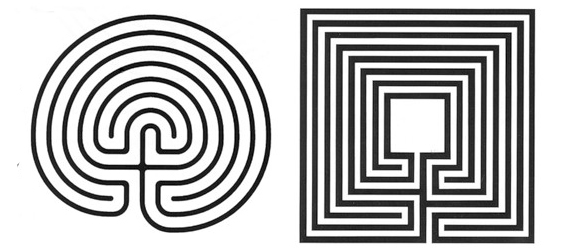                                                 Рис. 1

Примеры классических лабиринтов

     Различные формы лабиринтов (чаще всего круглой или прямоугольной формы)   встречаются по всему миру: от Америки до Австралии, от Азии до Скандинавии и Соловецких островов. Так же, например, как по всему миру, в культурах, изолированных друг от друга и никак не пересекающихся, встречаются изображения драконов.

Рис. 2

Лабиринт из Южной Индии

     Так, например, в древнем Египте предполагалось, что гробница фараона, помещенная в центре лабиринта, надежно предохранена от разграбления. Если кому-нибудь и удастся до нее добраться, то выбраться обратно и унести похищенное все равно не получится. 

 

     К. Германн, например, представляет лабиринт, воплощением обряда  инициаций – символической смерти и нового рождения. 

     «Давайте повнимательнее посмотрим на форму лабиринта – это внутреннее пространство, отделенное от остального мира. Это пространство окружено внешней стеной, в которой имеется лишь одно небольшое отверстие для входа. Прежде чем вступить в лабиринт, человек преодолевает целый ряд препятствий, и способным их преодолеть оказывается лишь тот, кто уже достиг зрелости. Когда вход остается позади, человеку открывается «принцип извилистой дорожки». Внутреннее пространство заполненно максимально возможным количеством поворотов – что означает огромную потерю времени, а также физическую усталость человека на пути к цели, т.е. к центру. Несколько раз человек приближается к цели только затем, чтобы дорожка вновь отвела его в противоположную сторону, и это вызывает большое психологическое напряжение. А поскольку на пути к центру идущий лишен возможности выбора, тот, кто в состоянии вынести это психологическое напряжение, непременно достигнет цели. В этом – символическое отображение необходимости следовать законам природы, отрицающее роль субъективного, произвольного подхода. Достигнув центра, человек остается в полном одиночестве, наедине с самим собой, с божественным принципом, с Минотавром или же с чем-то другим, чем может быть наполнено содержание понятия «центр». 

     Что бы выйти за лабиринта, человек должен повернуться и возвращаться назад по своим же следам. Поворот на 180 градусов означает не что иное, как наибольшее возможное отступление от собственного прошлого. Между дорогами к центру и от центра лежит ключевой, основопологающий опыт. Поэтому поворот в противоположную сторону – это не просто отрицание предшествующего опыта, это еще и новое начало. Человек, выходящий из лабиринта, совсем не тот, кто входил в этот лабиринт, – это человек, переродившийся для нового уровня существования. Именно в центре лабиринта происходит смерть и новое рождение.

     Смерть в ритуалах означает конец жизненного пути человека, после чего новообращенный рождается для иного существования. Это значение лабиринта находит свое отражение в его извилистой форме, в постоянной смене направлений слева (направление, противоположное движению солнца, т.е. движение к смерти) направо (направление движения солнца, т.е. к жизни)».

Рис. 4

Меандр

 

     Тут следует пояснить, что часто за лабиринты принимают меандры. Они также основаны на «принципе извилистой дорожки», но у них нет внешней ограничительной стены, они не являются замкнутой формой и не имеют четко выраженного центра. Также в меандрах часто имеются пересекающиеся ходы.

Рис. 5

Двойной меандр может трансформироваться в круглый семикольцевой лабиринт

 

     Кроме меандров и спиралей, иногда лабиринтами называют мэйзы. 

     Мэйз (от англ. maze) или лабиринт-путаница,– такое построение должно предлагать несколько ходов на выбор. Мэйзы бывают односвязные и многосвязные (рис. 6.1). Лабиринт же – построение, в котором существует только один ход (рис. 6.2). 

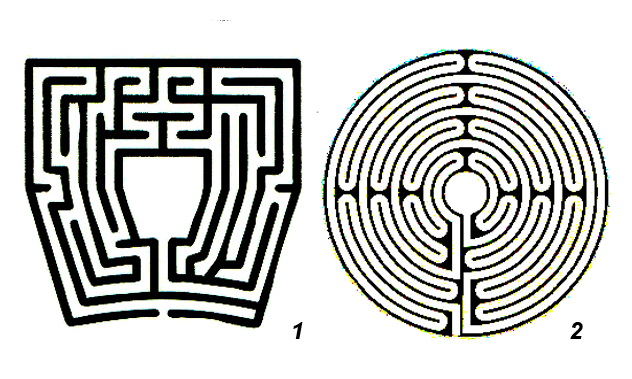  Рис. 6

                       

     Интерес к лабиринтам не угас и в последующие столетия, хотя и потерял свою мистическую окраску. Лабиринты стали излюбленным средством украшения садов и парков, своеобразным аттракционом.

Рис. 7

Церковный напольный лабиринт с крестом в центре 1533 г. (г. Гент, Бельгия)

 

     Однако, сама задача о лабиринтах долгое время считалась неразрешимой: полагали, что не существует надежных и точных правил, выполняя которые можно пройти любой лабиринт.

      Но за дело взялись математики – и задача была решена. Оказалось, что «безвыходных» лабиринтов нет и быть не может. Были выработаны правила, пользуясь которыми можно войти в любой, даже самый сложный и запутанный лабиринт и благополучно из него выбраться. 

Рис. 8

Каббалистическая схема

Образ мира, составленный из инициалов десяти «сефирот» (эманаций Бога), начинается снаружи со слов «кетер Элион» (евр., «высший венец») и идет по направлению к центру: «хохма» (евр., «мудрость»), «бина» (евр., «разум»), «хесед» (евр., «любовь»), «гвура» (евр., «сила»), «тиферет» (евр., «красота»), «нецах» (евр., «вечность»), «ход» (евр., «величие»), «иесод» (евр., «основание всех сил, действующих в Боге»). Движение заканчивается в центре самым маленьким инициалом – «малкхут» (евр., «царство»). Схема взята из каббалистического сочинения Моисея Кордоверо (1522-1570) «Пардес Риммоним», завершенного в 1549 г. и напечатанного в 1592 г. Дж. Борд ошибочно называет эту схему лабиринтом

 

     Итак.

     Перед вами – лабиринт (рис. 9). Сможете ли вы, войдя в него, пройти по всем галереям и благополучно вернуться обратно – туда, откуда началось ваше «путешествие»?

 Рис. 9

 

     Это будет не трудно, если идти в лабиринте не как придется, а по определенной системе.

     «Правило одной руки». Возьмите карандаш и «войдите» в лабиринт, ведя карандашом линию у одной из его стенок, например, у правой. Куда пойдет правая стенка, туда и ведите карандаш, «заходя» во все попадающиеся на пути разветвления, посещая все тупики и снова выбираясь из них, так, как если бы вы шли по настоящему лабиринту, не отрывая правой руки от его стенки… 

     Если вы будете достаточно внимательны, то обойдете весь лабиринт, побывав при этом и в камере с точкой, и вернетесь обратно.

     Предположим теперь, что вы хотите кратчайшей дорогой проникнуть в камеру с точкой. Достаточно ли для решения задачи «правила одной руки»? 

     Нет. 

     Что бы найти кратчайший путь, вы должны внимательно просмотреть весь маршрут, последовательно вычеркивая одну за другой все лишние петли, которые вы делали, заходя в разветвленные тупики. 

     Постарайтесь проделать это, отыщите кратчайший путь в камеру с точкой. 

 Рис. 10

 

     На рисунке 10 – тоже лабиринт. Он заметно проще предыдущего, не правда ли? Однако, если вы обойдете его, пользуясь «правилом одной руки», как это вы только что делали, то обнаружите, что в некоторых галереях (на рисунке они заштрихованы) так и не побывали! Почему же так получилось? 

     Дело в том, что этот лабиринт существенно отличается от лабиринта на рисунке 9. Его стенки не представляют собою единой геометрической сети. Сейчас мы поясним, что это значит.

     Если какая-нибудь точка, движущаяся по системе разветвленных и пересекающихся линий, может прийти к любой другой точке, не покидая линий, то такую систему называют геометрической сетью. Примеры вы найдете на любой географической карте – сеть железных дорог или шоссейные дороги… Но, скажем, реки и озера, если все они не соединены между собой каналами, не образуют единой геометрической сети.   

     Стенки второго нашего лабиринта также не образуют собой единой геометрической сети. Линии, проведенные жирно, образуют малую сеть, полностью изолированную от большой. На рисунке это хорошо видно. 

     Итак, решив две задачи, мы узнали о «правиле одной руки» следующее:  

     1) пользуясь им, можно обойти все галереи лабиринта и вернуться в исходную точку, если стенки лабиринта представляют собой единую геометрическую сеть;

     2) если стенки лабиринта образуют две (или более) геометрические сети, то, пользуясь этим правилом, можно обойти лабиринт и вернуться обратно, но некоторые галереи останутся в стороне от нашего маршрута, мы в них не попадем;

     3) «правила одной руки» недостаточно для того, чтобы найти кратчайший путь между двумя точками лабиринта. 

     Следовательно, обладая бесспорной практической ценностью (ведь оно выведет все-таки из любого лабиринта!), правило это является все же частным и не решает задачи о лабиринтах в общем виде. 

   Рис. 11

 

     Возьмите карандаш, войдите в лабиринт (рис. 11) и обойдите его, пользуясь «правилом правой руки». Вам будут встречаться буквы. Выписывайте их по порядку и тотчас же зачеркивайте на лабиринте, чтобы не прочесть одну и ту же букву дважды (ведь по каждой галерее вы пройдете два раза: один раз – туда, другой – обратно). 

     Буквы – для самоконтроля. Если вы нигде не собьетесь, то сможете прочесть строку из популярной песни. 

     Вернувшись в исходную точку маршрута, вы обнаружите, что не побывали во многих галереях… Оказывается, на рисунке не один лабиринт, а два. Своими разветвлениями они как бы вставлены один в другой и нигде между собой не сообщаются. 

 

     Обойдите с карандашом и другой лабиринт. Можете усложнить задачу – обойдите этот лабиринт вдоль левой стенки, а получившуюся в результате выписывания букв фразу прочтите в обратном направлении – справа налево.

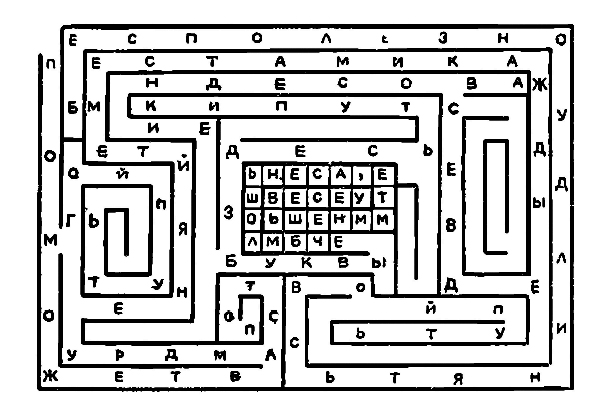 Рис. 12

 

     В центре лабиринта – спираль, в клетках которой что-то написано… Но текст зашифрован. Чтобы разобраться в зашифрованной фразе, нужен ключ к шифру, а он… спрятан в лабиринте. Найдите кратчайший путь к центру лабиринта, тогда отыщется и ключ (рис. 12). 

 Рис. 13

 

     На рисунке 13 – план лабиринта, считавшегося в XVII веке одним из красивейших сооружений подобного рода в Англии. Он занимал площадь около одной десятой гектара и представлял собой сад с аллеями и изгородями.  

     Посетители добирались до центра и выходили из сада, пользуясь «правилом правой руки». 

     Любопытно, что в саду имелась аллея, в которую никто из посетителей не попадал, и владелец сада мог отдыхать здесь без помех… 

     Сможете найти эту укромную аллею?

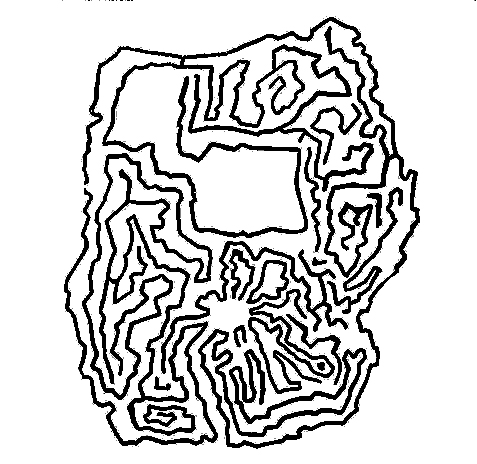 Рис. 14 

 

     На рисунке 14 – план лабиринта, описанного в приключенческой повести «Остров тайн».

     …На необитаемом острове в одной пещере находилась лаборатория, в которой долгие годы работал старый профессор. Вначале он добирался до лаборатории, пользуясь «правилом правой руки», а затем – кратчайшим путем, который вскоре отыскал. 

     Но вот на острове появляется морской бродяга Том Кент, ставший жертвой кораблекрушения (его спас профессор). 

     Тома больше всего интересуют алмазы в уникальных приборах лаборатории. Починив разбитую штормом шлюпку, он похищает несколько алмазов и покидает остров. 

     Полагая, что Том Кент снова возвратится на остров (к тому же, возможно, не один), профессор решает обезопасить лабораторию от непрошеных визитеров. Как это сделать? Забаррикадировать какой-нибудь проход? Но тогда он и сам не сможет пользоваться свободным входом и выходом…

     Вспомнив, что Кент ходил по лабиринту только по «правилу правой руки» и никакого иного пути не знал и даже не догадывался о его существовании, профессор разобрал в одном месте лабиринта стенку, перегораживавшую галерею. Когда Кент с приятелями и в самом деле вернулся на остров в надежде поживиться оставшимися у профессора алмазами, он не смог проникнуть в лабораторию. Много раз обходил все галереи, коридоры и закоулки лабиринта, следуя вдоль правой стенки, и всякий раз неизменно возвращался к выходу, не обнаружив лаборатории.  

     Попробуйте отыскать на плане кратчайшую дорогу профессора, затем путь, которым добирался до лаборатории Том Кент, а также подумайте о том, где именно профессор мог разобрать стенку, что бы добиться желаемого результата. 

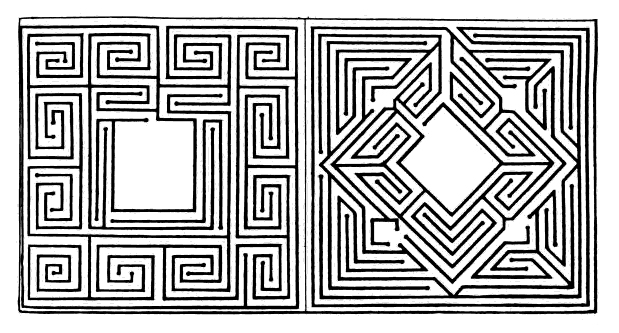 Рис. 15.1

 

Рис. 15.2

 Георг Андреас Беклер (работал ок. 1644-1698). Десять проектов садовых лабиринтов из книги «Новые архитектурные достопримечательности»

 

 

Как выбраться из самого сложного лабиринта?

     Правила хождения по лабиринтам, сформулированные французским инженером Тремо, пригодны для любого лабиринта, как бы велик и сложен он ни был. 

     Сами по себе правила очень просты. К тому же они освобождают от необходимости запоминать что-либо – дорогу, число поворотов и т.п. и могут приниматься автоматически, при одном, правда, непременном условии: идя по лабиринту, нужно маркировать свой путь – отмечать вход в каждую посещаемую вами галерею и выход из нее. 

     Приводим правила Тремо.

     Вступив в лабиринт, доходим до первого перекрестка и направляемся по любой галерее. Куда может привести эта галерея? Очевидно, либо в тупик, либо на новый перекресток,– третьей возможности нет. Если галерея кончается тупиком, мы возвращаемся обратно, делаем на выходе вторую отметку (первую мы сделали, войдя в нее) в знак того, что путь этот уже пройден нами дважды и теперь выключается из дальнейшего маршрута. Если же галерея не заканчивается тупиком, а приводит к новому перекрестку, мы опять входим в любую галерею и идем по ней. 

     Так идем мы по лабиринту, выбираясь из тупиков и произвольно выбирая галереи на перекрестках, пока эти перекрестки нам незнакомы, т.е. посещаются нами впервые. Но рано или поздно мы попадаем на уже знакомый нам перекресток, именно на такой, где мы уже побывали. Мы узнаем об этом по нашей пометке у входа в какую-нибудь из вливающихся в перекресток галерей. 

     Выйдя на знакомый перекресток, мы теряем свободу выбора направления,– вступают в силу три правила Тремо. 

     П р а в и л о   п е р в о е. Если на знакомый перекресток привела галерея, по которой мы прошли только раз, то мы должны тотчас вернуться по ней на предыдущий перекресток и войти в другую галерею. 

     П р а в и л о   в т о р о е. Если мы пришли на знакомый перекресток дорогой, которой уже до этого однажды прошли, а теперь она, следовательно, пройдена вторично,– мы не можем по ней возвратиться на предыдущий перекресток, т.к. это было бы третье прохождение по одному и тому же участку пути, что противоречит условиям применения правил. В этом случае мы должны войти в такую галерею, в которой еще не были совсем, а если среди вливающихся в перекресток галерей нет такой, то в такую, по которой прошли только один раз (т р е т ь е   п р а в и л о). Разобраться в этом помогают наши пометки: отсутствие пометок у входа в какую-нибудь галерею свидетельствует, что в нее мы еще не входили, одна пометка указывает, что галерея однажды уже пройдена, а две пометки равносильны запретительному знаку – эта галерея уже пройдена нами дважды, «вход воспрещен». 

     Строго соблюдая эти, сами по себе очень простые, правила, можно обойти все галереи любого, даже самого сложного лабиринта, и благополучно возвратиться в исходный пункт. Подчеркиваем – все галереи. В этом и заключается отличие правил Тремо и их преимущество: как мы уже знаем, «правила одной руки» достаточно, чтобы не заблудиться, но оно не дает уверенности в том, что в маршрут обхода вошли все до одной галереи лабиринта. 

 Рис. 16

 

      Рассмотрим три правила Тремо на примере (рис. 16). На чертеже нет необходимости маркировать входы в галереи и выходы из них какими-либо значками, т.к. виден сам путь, нанесенный пунктиром. Мы сразу можем определить, где прошли один раз, где – два, а где вовсе еще не были. 

     От тщательности маркирования маршрута прежде всего зависит успех исследования лабиринта или пещеры, а иногда, может быть, и судьба исследователя. 

     Лабиринт начинается перекрестком А. Идем, куда нам вздумается, произвольно. Вступаем в галерею 1, проходим перекрестки Б, В, Г. Так же произвольно выбирая направление, входим в галерею 2. Это, оказывается, тупик… Возвращаемся на перекресток Г. Теперь это уже знакомый перекресток, и мы не можем покинуть его, произвольно выбрав направление, сейчас мы должны применить одно из трех правил. Какое же именно? Применить первое правило нельзя, т.к. галерея 2, которая привела нас сюда, уже пройдена дважды. Применяем второе правило – входим в галерею 3, в которой еще не были.  Галерея 3 приводит на незнакомый перекресток Д; здесь можно выбрать направление произвольно. Проходим галерею 4 и оказываемся на уже знакомом нам перекрестке А. Применяем первое правило – возвращаемся на перекресток Д; подчиняясь второму правилу, заходим в тупичок 5, снова выходим на перекресток Д и согласно третьему правилу идем по галерее 3… 

     Проследите маршрут до конца, обращая особое внимание на знакомые перекрестки, где направление дальнейшего маршрута определяется применением того или иного из трех правил. 

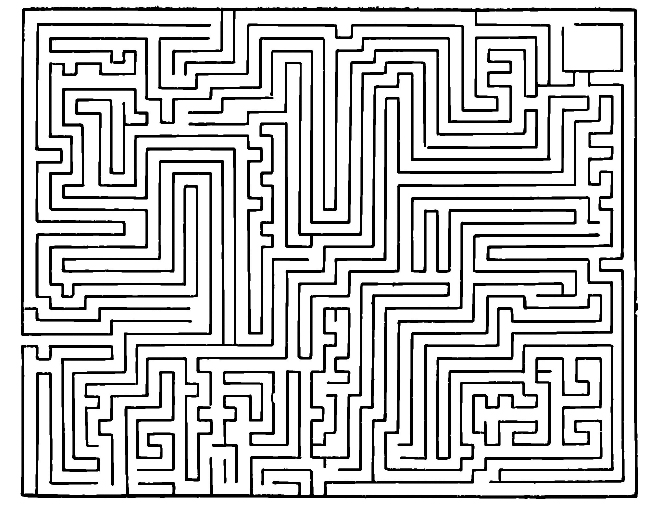  Рис. 17

 

     Для желающих потренироваться помещаем план большого и сложного лабиринта-путаницы (рис. 17). Обойдите его по «правилу одной руки», поищите затем кратчайший путь. Попробуйте обойти лабиринт, применяя правила инженера Тремо. Будьте очень внимательны: успех зависит только от этого… 

                     

     Как вы думаете, это тоже лабиринт (рис. 18)?

     Возможно, вы и правы. Но здесь изображен всего-лишь многоугольник – неправильный невыпуклый многоугольник с очень сложным контуром. Почему бы ему не быть вместе с этим и лабиринтом? 

     Если напрячь внимание, можно составить себе общее зрительное представление об этой фигуре. Попробуйте. Проверьте себя, затушевав слегка площадь многоугольника. 

  Рис. 18

   

     Возможно, вы и правы. Но здесь изображен всего-лишь многоугольник – неправильный невыпуклый многоугольник с очень сложным контуром. Почему бы ему не быть вместе с этим и лабиринтом? 

     Если напрячь внимание, можно составить себе общее зрительное представление об этой фигуре. Попробуйте. Проверьте себя, затушевав слегка площадь многоугольника. 

Рис. 19

Глиняная табличка с одним из древнейших изображений лабиринта, найденная среди руин микенского дворца в Пилосе, Южная Греция. Ок. 1200 г. до н.э.

Рис. 20.1

Рис. 20.2

Девять лабиринтовых фигур (фигурных лабиринтов). Гравюры на дереве (XVI в.) архитектора Франческо Сегалы, опубликованные в его «Книге лабиринтов Франч. Сегалы, падуанского скульптора и архитектора» («Libro de laberinti de Franc. Segalla Padoano Scultore et Architettori»), которая содержит большое количество подобных изображений. Издание хранится в Апостолической библиотеке в Ватикане. Это единственные факты, которые удалось почерпнуть в самой библиотеке и в эссе А. Омодео

 

     Конечно, эта статья не исчерпывает всей богатой и древней истории лабиринтов. Конечно, лабиринт эволюционировал (рис. 19) и усложнялся (рис. 20.1 и 20.2), но при этом оставался «неизменен» и «верен себе». Интересен и тот факт, что за несколько тысячелетий лабиринты по-прежнему привлекают, интересуют и увлекают людей. 

 

См. также: 

 

►►►  "Всё о ребусах":

https://www.liveinternet.ru/users/epigone/blog#post413843802

 

►►►  "Тайны криптограммы":

https://www.liveinternet.ru/users/epigone/post440863029/

 

 

 

Ответы:

 

Рис. 9. Решение на рисунке 21.

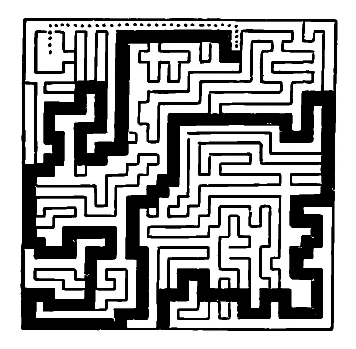     Рис. 21

 

Рис. 11. В одном лабиринте можно прочесть: «Кто ищет, тот всегда найдет», во втором – «Смекалка во всяком деле выручит». 

 

Рис. 12. В лабиринте можно прочесть: «Поменяйте местами каждые две соседние буквы». Следуя совету, в центре лабиринта вы прочтете загадку: «Чем больше нас, тем меньше весу» (ответ: «дырки в сыре»).

 

Рис. 13. На рисунке 22 точкой отмечена аллея, в которой владелец сада укрывался от досужих посетителей лабиринта. 

  Рис. 22

 

Рис. 14. На рисунке 23 точками указан кратчайший путь в лабораторию, которым пользовался профессор.

Буквой А помечена стенка которую разобрал профессор, чтобы помешать Тому Кенту.

Возможны и другие решения.

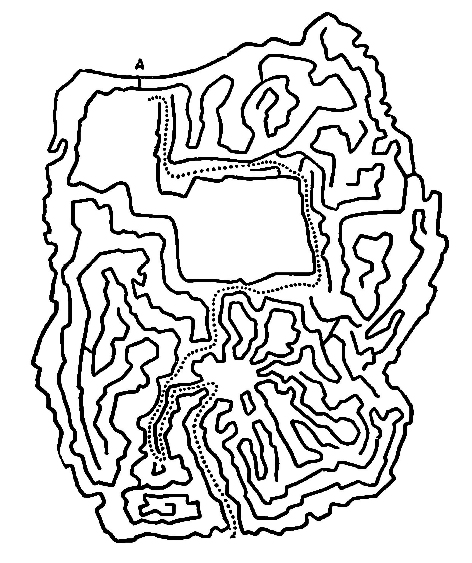  Рис. 23

 

 

 

По материалам книг К. Германна «Лабиринты мира» (Kern Hermann «Through the Labyrinth», Prestel Verlag, Munich, 2000); Дж. Саварда «Лабиринты» (Jeff Saward «Labyrinths and Mazes», Gaia Books Limited, 2003); В. В. Акентьева «Со второго взгляда», Лениздат 1969 г.