начало исследований тут:
https://www.liveinternet.ru/users/2851019/post511403731/
https://www.liveinternet.ru/users/2851019/post511470954/
Рассмотрим последовательно все слои и связи внутри рунного круга.
Всего у нас три числовых группы, в каждую входят по 12 рун, то есть каждая из 12 рун имеет одиннадцать связей с другими рунами внутри своей числовой группы.
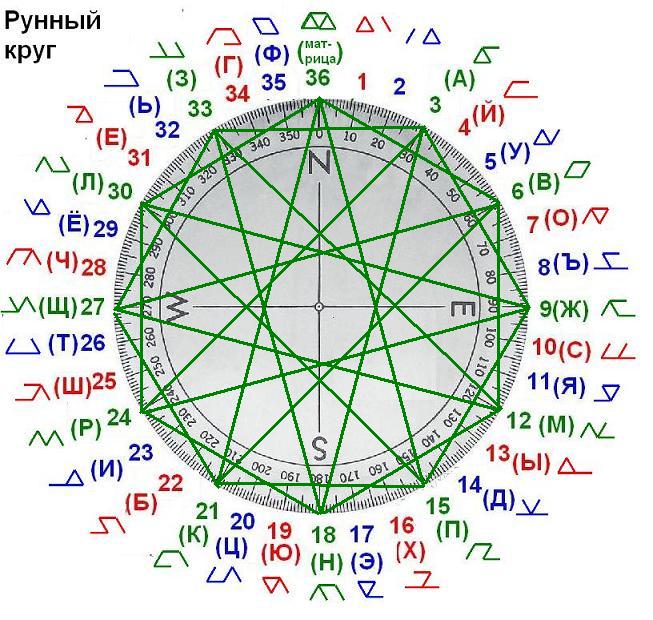
Вот так выглядят все 12 рун (на примере рун первой группы), объединённых в единое облако- близкая к кругу фигура.
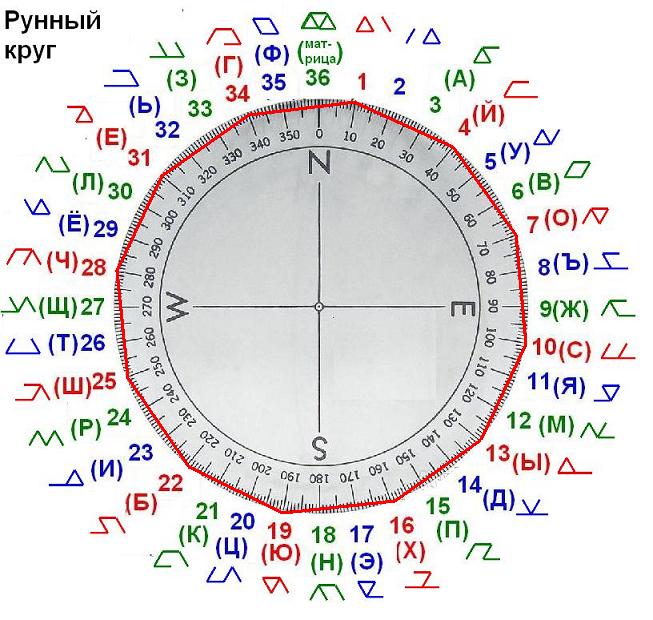
а вот так происходит переплетение трёх двенадцатигранников. Это напоминает мне про нади, состоящую из трёх отдельных жил.
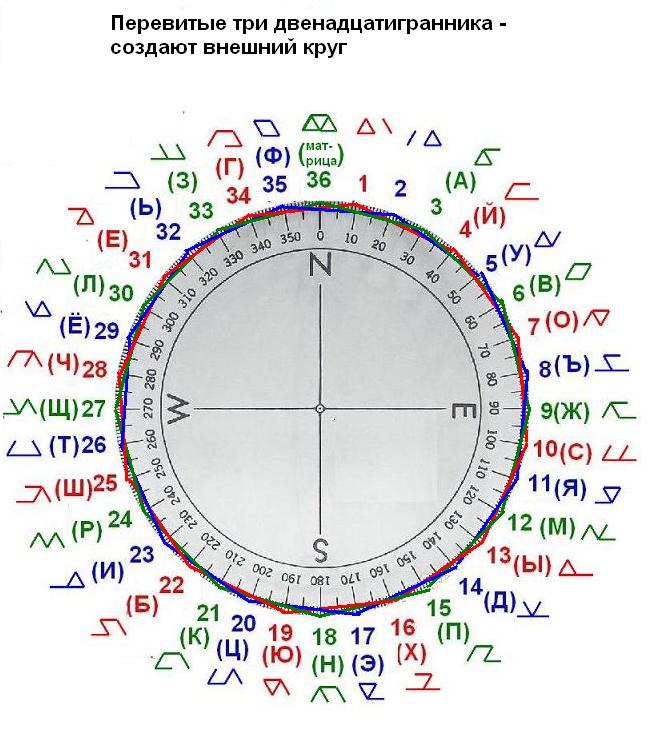
как круг со всплесками - шишечками, узлами отдельных рун.
Следующая большая фигура внутри числовой группы - это соты. Их две. Одна из них с рунами с чётным числовым значение, другая с нечётным. Это как разделения на инь-ян. Двойственность внутри числовой группы, которая, возможно , указывает на преобладание женской и мужской энергии внутри группы.
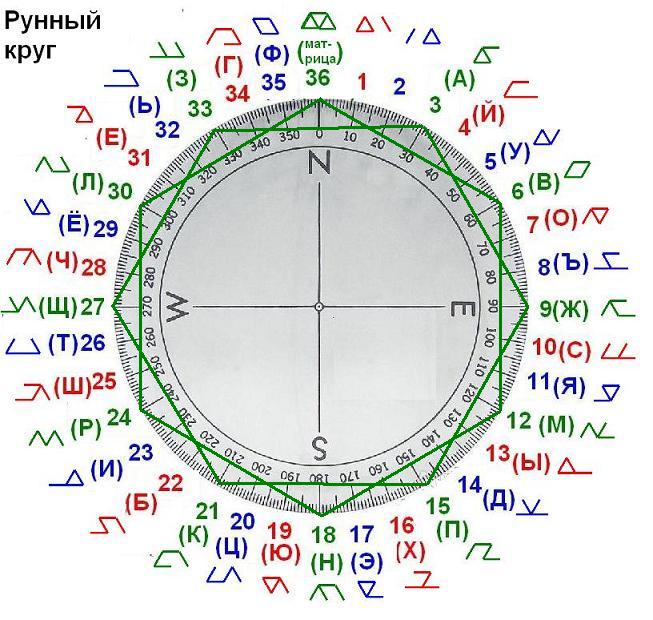
а вот такая фигура и заполнение слоя получается, когда все шесть сот вместе - новый круг внутри круга с более крупными треугольничками на нём.
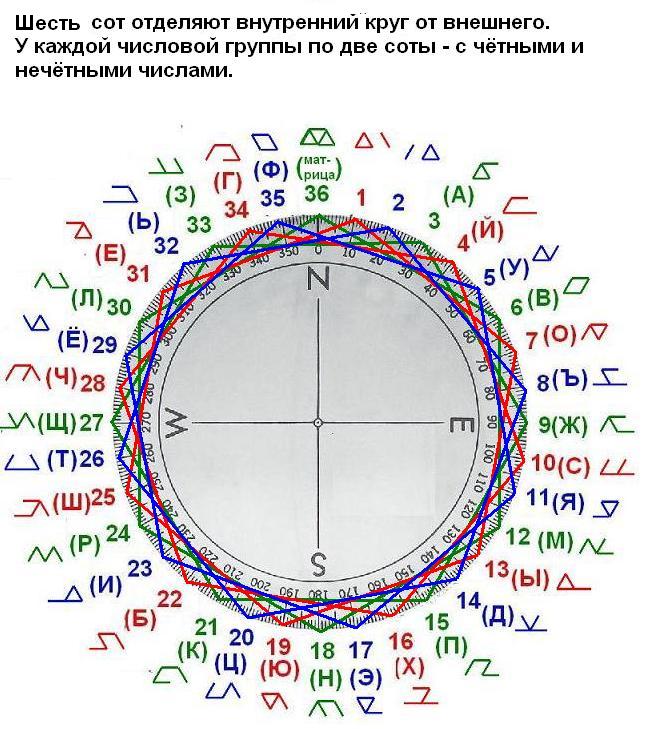
Дальше идут квадраты. В каждой числовой группе их три.
И мы помним что особенностью этих квадратов является то, что все числовые значения рун в них можно привести к единому цифровому корню.
Эти девять квадратов как бы делят круг на цифры от 1 до 9. Вводят десятичное счисление в мироздание? Также как соты вводят двоичное?
Ещё снова надо вспомнить о плоском торе, одно из названий которого квадратный плоский тор.
Будут ли эти квадраты задействованы в формировании его? Ну и вспомним про квадратуру круга...
https://pmc.ncbi.nlm.nih.gov/articles/PMC3358891/
"Геометрический тор — это поверхность вращения, полученная путём вращения окружности в трёхмерном пространстве вокруг оси, лежащей в одной плоскости с окружностью. Стандартная параметризация геометрического тора сопоставляет горизонтальные и вертикальные линии единичного квадрата с широтами и меридианами поверхности изображения. Этот единичный квадрат также можно рассматривать как тор: верхняя линия абстрактно отождествляется с нижней линией, а левая и правая стороны — с левой и правой сторонами квадрата. Из-за своей локальной евклидовой геометрии он называется квадратным плоским тором."
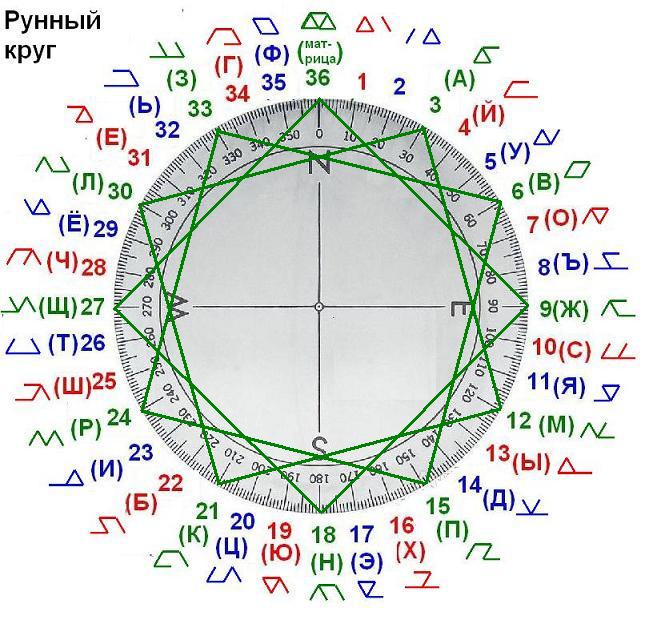И опять мы видим этот слой как круг со всё увеличивающимися треугольниками на нём.
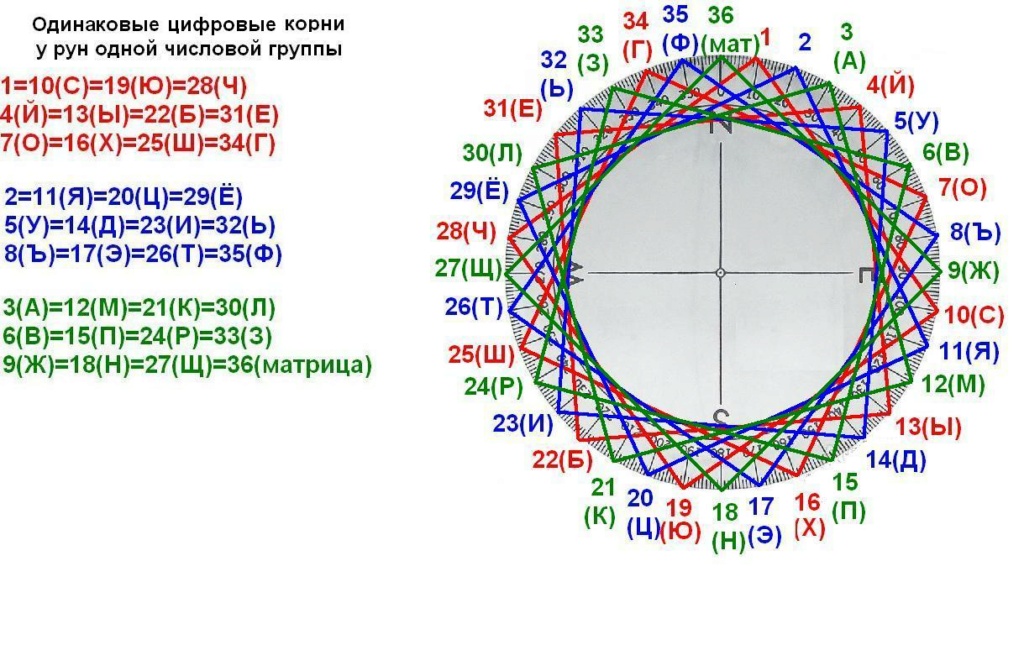
Круг следующего уровня образуется за счёт равносторонних треугольников. Их 12. И они также как и соты бывают с чётными, а бывают с нечётными числами-узлами. В каждой числовой группе их по четыре. Здесь есть перекликание с квадратами, которые тоже своими углами задействуют 12 узлов в одной числовой группе. То есть и квадраты и треугольники и соты в одной числовой группе - это всё Эрцгамма.
Лучи звезды становятся всё длиннее, чем уже внутренний круг.
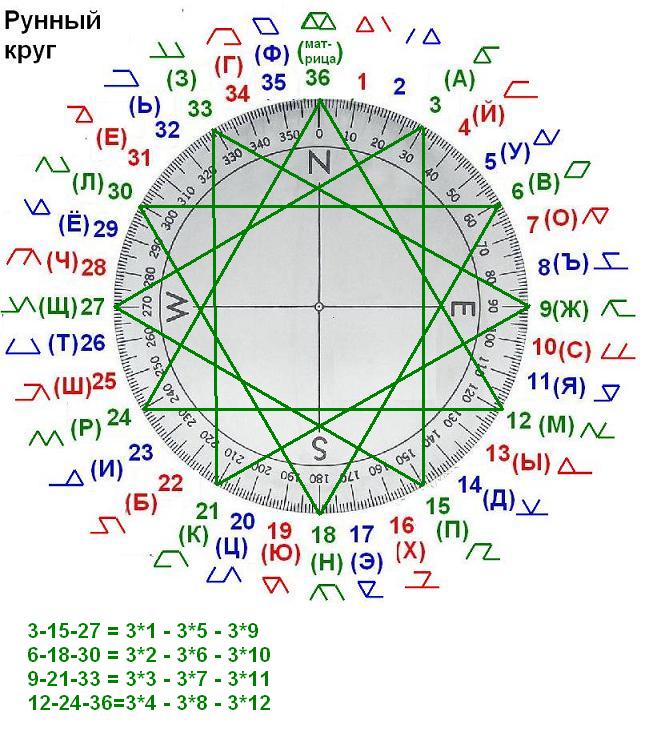
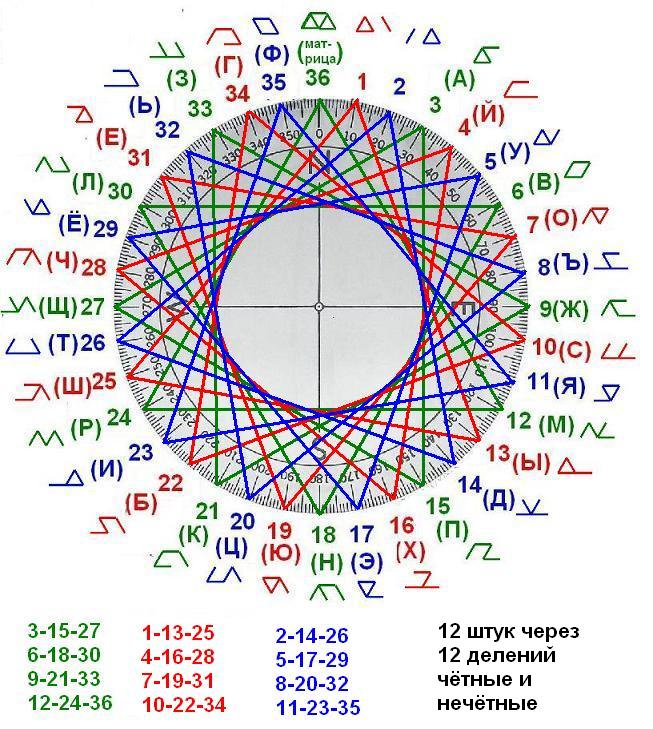
Ну и самый узкий внутренний круг образуется за счёт равнобедренных треугольников. Их также двенадцать в одной числовой группе и соответственно 36 в трёх числовых группах. Они также как и равносторонние треугольники вписаны в соту. Но не в "отдельную" соту, а которую сами и формируют, в отличие от равносторонних треугольников. Только их числа разнятся - если одно число в вершине чётное, значит два угла напротив с нечётными числами и наоборот. У них интересно то, что они создают как бы два круга - один - самый близкий к центру, а другой - близкий к краю.Как будто они могут самостоятельно сформировать тор, путём связывания между собой двух сот (чётной и нечётной) каждой числовой группы и формируя "дыру" внутри них.
