Факты о гексагональных сетках

В Gamelogic просто одержимы всевозможными клетками. Они создают инструментарий для их формирования, пишут про них, но на самом деле их одержимость заходит гораздо дальше (даже бывают «Пятницы футболок в клетку»).
Они поделились интересными (и непонятными) фактами на страницах Gamasutra, на которые мы наткнулись в своей миссии по изучению всего и вся про клетки и их применение в играх. В этом переводе статьи подробнее описаны принципы сеток из шестигранных клеток.
Если вы хотите приобщиться к клеточному движению, следите за твиттером @gamelogicZA или ищите хэштег #fungridfacts.
Примечание: Здесь представлены образцы некоторых занимательных фактов о шестиугольниках. В качестве более серьёзного и детального математического взгляда на шестигранные клетки авторы создали PDF-документ, освещающий множество аспектов, о которых вы больше нигде не прочтёте, с особым упором на вещи, касающиеся игровой разработки: определение формы на шестигранной сетке через простые уравнения (для треугольников это max(x, y, z) < r), скалярные и векторные произведения для упрощённой тригонометрии, матрицы переходов, шестигранный аналог дерева квадрантов, процедурная генерация (с аналогом шума Перлина) и представление сеток из треугольников, ромбов и пятигранных лепестков.
Скачать его можно здесь: https://www.gamelogic.co.za/downloads/HexMath2.pdf (англ.).
Пример изображения из файла:

Агон – старейшая из (известных нам) игр с шестигранными клетками
Использовать шестиугольники в играх стали относительно недавно. Насколько мы знаем, первой из таких игр является Агон, или «Стража королевы». Она появилась в 18 веке во Франции и стала популярной благодаря простым правилам и комплексной стратегии: у каждого игрока есть королева и шесть стражников. Игроки решают, кто ходит первым, затем ходят по очереди. Каждый ход двигается по одной фигурке. Цель – первым достичь центрального гекса (трона в центре поля) королевой и расположить всех стражей вокруг неё.
Джон Нэш (тот самый из «Игр разума») заново изобрёл игру гекс в целях подтверждения «стратегии заимствования стратегии»
Гекс – это стратегическая настольная игра на шестигранной сетке любого размера и нескольких возможных форм. Впервые была придумана датским математиком Питом Хейном в 1942.
Для победы игроку нужно первым соединить две своих противоположных стороны цепочкой фишек. Гекс не может закончиться вничью, один из игроков всегда побеждает. Единственный способ не дать оппоненту составить соединяющую цепочку – составить собственную.
Джон Нэш самостоятельно изобрёл игру в 1947. Он продемонстрировал, что первый игрок может добиться победы с помощью принципа заимствования стратегии. Любой дополнительный ход только улучшит положение любого игрока. Поэтому, если у второго игрока есть выигрышная стратегия, первый может её позаимствовать. Для этого первый ход делается как угодно, а затем копируются ходы второго игрока. Даже, если стратегия предполагает ход на уже занятую клетку, можно просто сделать произвольный ход. Это гарантированно принесёт победу первому игроку.
Для набросков алгоритмов и механик игр с шестиугольниками можно использовать кирпичную сетку
Рисование сильно помогает при разработке алгоритмов и механик, но рисовать гексы не очень удобно. Конечно, можно распечатать шестигранную сетку, но если идея приходит в голову внезапно (или вы просто много рисуете, как и я сам), приходится быстро рисовать шестиугольники. Один из вариантов – рисовать кирпичи, как на картинке ниже. Это намного проще, а вся топологическая информация сохраняется: у каждого кирпича есть шесть соседей, расположенных с тех же сторон.

Площадь любого параллелограмма с вершинами на шестиугольных клетках равна целому количеству гексов
Напомним, что площадь параллелограмма в обычном евклидовом векторном пространстве со сторонами, заданными векторами (x1, y1) и (x2, y2), равна |x1y2 – x2y1|.
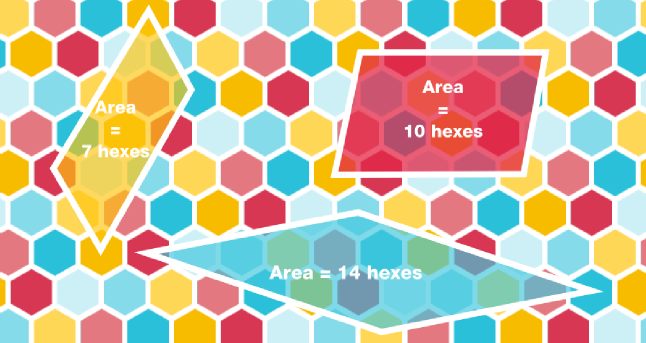
Следовательно, если все элементы формулы – целые числа, то и площадь будет целым числом. При сдвиге точек, параллельных оси x, площадь параллелограмма остаётся прежней, так что, если сдвиг вызван заменой прямоугольной решётки на шестиугольную, площади параллелограммов рассчитываются так же, как и на прямоугольной решётке, а значит тоже должны быть целыми числами.
Из этого факта следует, что площадь любого треугольника с вершинами на гексах равна половине целого числа гексов (поскольку площадь треугольника равна половине площади параллелограмма). Следовательно, любой многоугольник с вершинами на клетках имеет площадь, равную половине целого числа клеток.
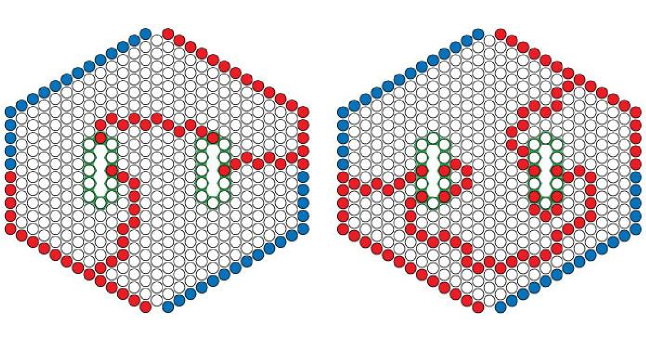
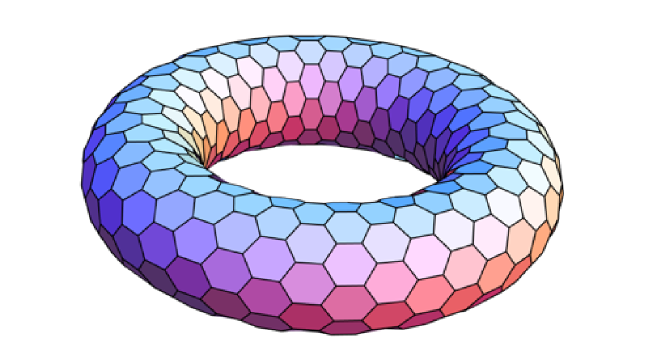
Свёрнутая прямоугольная сетка – это тор, как и свёрнутая шестиугольная
Поскольку дисплеи прямоугольные, идея прямоугольного сворачивания вполне естественна – что уходит в одну сторону, появляется с другой. Не так просто сразу сообразить, как аналогичным образом свернуть шестигранную сетку. На самом деле, это можно сделать несколькими способами, в зависимости от формы сетки.
Сетка в виде параллелограмма сворачивается почти так же. как и прямоугольная. Можно легко представить её топологическое соответствие тору. Для сетки в форме шестиугольника всё уже интереснее. В данном случае, уйдя за одну грань, вы появитесь с противоположной. Но, в отличие от прямоугольника, вы пересечёте шестиугольник дважды, прежде чем появиться в начале пути. Это не очень легко представить, но это тоже топологически соответствует тору. На рисунке ниже показано, как всё работает:
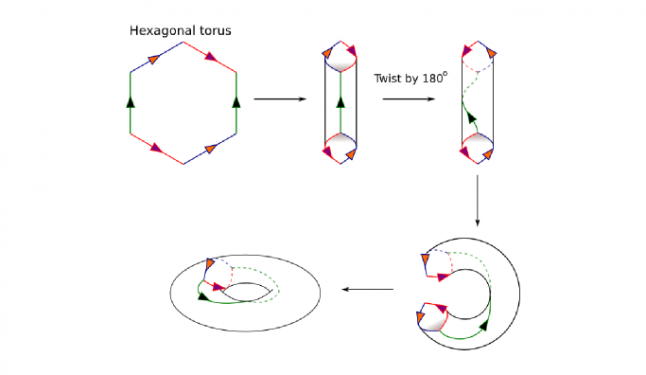
Существует только один магический шестиугольник, состоящий более, чем из одной клетки
Существуют магические квадраты любого порядка с числами от единицы до итогового количества клеток. Но, за исключением одноклеточного, существует лишь один такой магический шестиугольник (если не брать в расчёт отражения и вращения).

Магические фигуры с последовательностями целых чисел, начиная от единицы, называются нормальными. Аномальные магические фигуры содержат последовательности, начинающиеся с другого целого числа. Если говорить об аномальных магических шестиугольниках, то их будет больше.
Ромбододекаэдральные соты – трёхмерные родственники шестиугольной сетки среди заполняющих пространство многоугольников
Вокруг одного круга можно вплотную разместить ровно шесть кругов такого же радиуса. Можно предположить, что и сферы возможно разместить так же плотно. Однако, нет – мы может прислонить к центральной сфере 12 сфер, при этом останется довольно много места, но 13-ю поместить уже будет некуда (это называют проблемой контактных чисел).
Ромбододекаэдральные соты – это заполнители трёхмерного пространства. Это разбиение Вороного кубической гранецентрированной упаковки, считающейся самым плотным заполнением обычного пространства одинаковыми сферами. Гранецентрированная упаковка – это размещение одинаковых шаров (к примеру, пушечных ядер) при их складировании.

Квадраты и треугольники скользят, а гексы – нет
Поэтому гекс-тетрис и не особо популярен – палка из гексов не пролезает в оставленное для неё место.
Эту проблему можно обойти, уменьшив размер шестиугольников или же заменив их кругами. Круги будут соприкасаться, но в то же время скользить, что и требуется в подобных играх.
Шестигранная сетка может служить основой для треугольной
Гексы и треугольники связаны друг с другом, как показано на картинке. Фокус в том, чтобы использовать единую окраску из трёх цветов: один для направленных вверх треугольников, другой для направленных вниз и третий для вершин.

Если вы до этого не работали с треугольными сетками, вы не сразу поймёте, насколько это облегчает математику. Треугольные сетки часто скоординированы довольно нескладным образом, и у вас не получается применять векторные вычисления для решения простых геометрических задач, как в случае с квадратами и гексами. Например, при схеме, как на рисунке, не удастся получить вектор «смещения» для вычисления движений. Однако, если в схеме на заднем плане присутствуют гексы, вы можете пользоваться элегантной векторной математикой для смещений и непостоянных форм, а также выполнять вращение и отражение с помощью умножения матриц.
Lego-образные гексовые блоки бывают двух видов – обычные и боковые
Конструкционные блоки из шестиугольников открывают интересные возможности в дизайне. Ниже показаны два их вида.
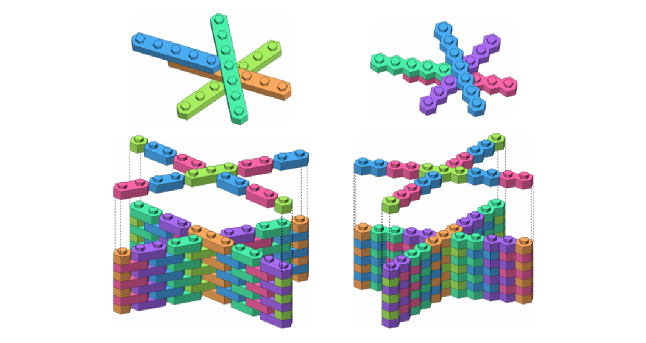
При грамотном расположении выемок и шипов можно соединять блоки не только «синхронно», как в самом конструкторе Lego, но и «несинхронно».
Края можно оставлять открытыми, чтобы шипы было можно помещать и в «полувыемки».
Также можно сделать соединительные блоки, чтобы квадратные и шестиугольные блоки работали совместно.
Шестиугольные клетки могут обеспечить структурную целостность марсианских зданий
Да, жилища из шестиугольников – не прерогатива пчёл.
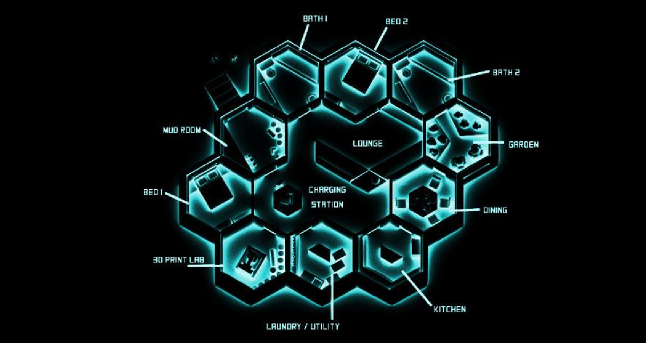
На картинке выше показан дом Queen B, спроектированный для защиты людей от радиации и погодных условий Марса. Список особенностей дома с официального сайта:
- Полноценная кухня, 2 спальни, 2 ванных комнаты, сад, лаборатория 3D-печати, комната отдыха, прачечная и комната декомпрессии/прихожая в качестве стандартного набора.
- Дизайн с расчётом на удержание тепла и рельефная крыша, препятствующая скоплению мусора.
- Панели из обеднённого урана, снижающие радиацию до безопасного уровня.
- Привлекательная эстетика, помогающая в продвижении миссии и поиске добровольцев.
Последний пункт особенно важен для игр: дома из гексов помогут их продвигать :-)
Невозможно окрасить шестигранную сетку в два цвета, так чтобы соседние гексы всегда были разного цвета
Иногда это создаёт неудобства в играх, рассчитанных на двоих.

Впрочем, дополнительные цвета сразу решат проблему. Трёхцветная схема используется в шестигранных шахматах. Слон в такой схеме тоже ходит только по клеткам одного цвета, как и в обычных шахматах.
Сферу нельзя полностью покрыть одними шестиугольниками
Как минимум вам понадобится добавить 12 пятиугольников. Подобные сферические многогранники основаны на икосаэдре (правильный многогранник, состоящий из 20 треугольников), смотрите видео:
Есть множество других способов составления сфер из шести- и пятиугольников, и химия изучает их на примере фуллеренов (молекул углерода в форме сферы, цилиндра и т.п.).

Из шестиугольников можно выстраивать цилиндры, торы и даже ленты Мёбиуса.

Хоть вы и не можете выстроить сферу с помощью гексов, вы можете подделать её, сделав цилиндр или тор, с виду похожий на сферу. Один из таких приёмов работает в игре Antipod.

Другой приём использует свёрнутый шестиугольник (а значит тор), превращённый в полусферу, как сделали тут.
Полигекс – плоская фигура, состоящая из n шестиугольников, соединённых гранями, как в обычной шестигранной сетке
Фигуры в Тетрисе называют тетромино (четыре соединённых гранями квадрата в фигуре), это подвид полимино (любое число соединённых гранями квадратов в фигуре). Шестигранный эквивалент полимино называется полигекс.

Есть много головоломок на использование полигексов. В самых распространённых игроку требуется составить заданную форму из набора полигексов. Не существует формулы для вычисления количества полигексов заданного порядка.
Выбор между вертикально и горизонтально ориентированными гексами – не просто вопрос эстетики

Аргументы за и против:
- Горизонтальная ориентация схожа с раскладкой клавиатуры: для перемещения можно использовать WEADZX, также, как WASD на квадратной сетке. Однако, QWEASD прекрасно подходит для вертикальных клеток.
- Горизонтальная схема лучше подходит для 3D/изометрии, где нижний ряд ближе к игроку, а верхний дальше. Таким образом высокие спрайты не будут загораживать центр ближайших клеток, затрагивая только край. Вероятно, поэтому вертикальная ориентация лучше подойдёт для вида ровно сверху.
- Вертикально ориентированные клетки можно сделать вдвое шире, чем их высота, с точностью до пикселя. Ограниченная высота по сравнению с шириной добавляет глубины, особенно когда на гексах располагаются объекты, способные перекрывать стоящие позади клетки.
- В сетке вида NxN горизонтальная ориентация приведёт к увеличенной ширине, как у PC-мониторов. Иными словами, карта из горизонтальных клеток лучше подойдёт для широких экранов, благодаря относительно схожему соотношению строк и столбцов. В зависимости от размера и видимой области карты, это может дать игроку лучший обзор и позволит избежать лишнего скроллинга.
- С вертикальными клетками будут видны все стены. Если у вас горизонтальная ориентация и есть стены, идущие вдоль вертикальных линий, вряд ли получится обогатить их деталями (дверьми или проходами). Более того, если использовать вышеупомянутый тип перспективы, гексы будут выглядеть на порядок лучше, поскольку вы сделаете их приплюснутыми. Если сплюснуть горизонтальный гекс, уклон на вершинах получится не очень крутым (около 1/8 против 1/2 у вертикальных). Иными словами, если вы делаете вид с высоты птичьего полёта или применяете пиксель-арт, вертикальные гексы будут смотреться лучше.
Только три типа выпуклых шестиугольников могут заполнить плоскость (то есть выступать в качестве сетки)
Плоскость можно заполнить не только правильными шестиугольниками. Из выпуклых шестиугольников подходящими будут три типа, удовлетворяющих следующим условиям:
- A + B + C = 360, a = d
- A + B + D = 360, a = d, c = e
- A = C = D = 120, a = b, c = d, e = f
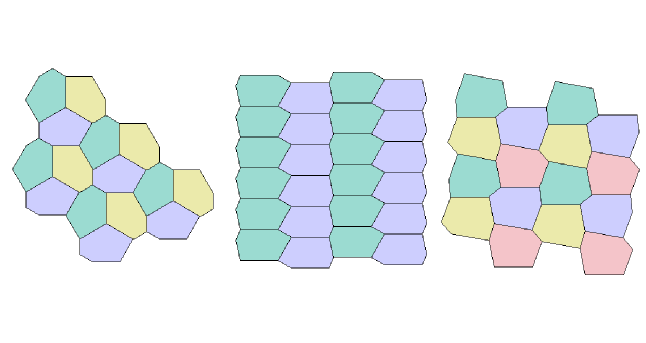
Поиграть с такими клетками можно здесь: https://www.geogebratube.org/student/m155779
Что касается пятиугольников, никто не знает, сколько разных типов фигур может заполнить плоскость (известно минимум о 14, но может быть и больше).
Вместо векторов в качестве координат гексов можно использовать комплексные числа
Координаты сетки можно представить в виде комплексных чисел. Для прямоугольной сетки это будут Гауссовы целые числа. Для шестигранной сетки это будут целые числа Эйзенштейна.
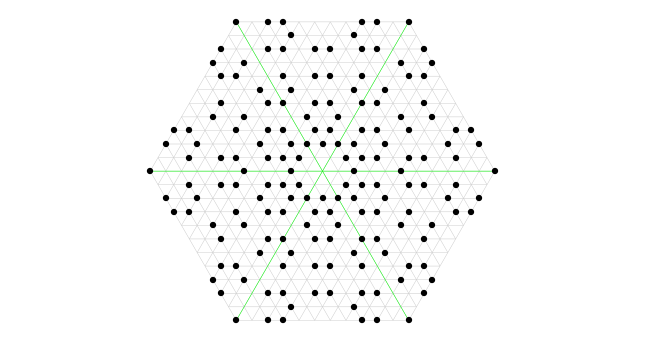
У этих чисел много общего с настоящими целыми. Например, у вас есть понятие о делении с остатком или без, так что можно определить простые числа, и, следовательно, выстроить полную теорию чисел.
Такие числа могут использоваться в реализации определённых алгоритмов, например, раскрашивания, формирующего составные блоки многих других алгоритмов.
Треугольная сетка – двойственная сетка шестиугольной
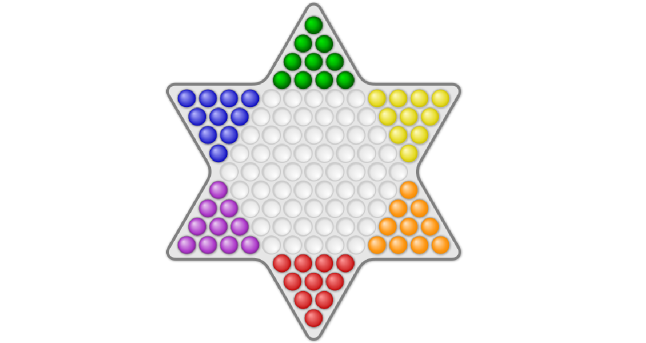
Это означает, что любая игра, разыгрываемая на вершинах треугольных клеток, на самом деле играется на гранях шестиугольников. Этот факт пригодится как в дизайне, так и в разработке алгоритмов (для реализации китайских шашек сама логика велит пользоваться шестигранной сеткой, а не треугольной!).
Использование треугольников вместо гексов позволяет снизить количество разных плиток в наборе
Многие плиточные игры спланированы так, чтобы их грани совпадали и таким образом выстраивались более крупные формы. Набор плиток при этом может быть очень обширным, и одним из решений проблемы является деление гексов на треугольники. Это серьёзно сократит количество необходимых плиток и будет особенно полезным в компьютерных играх, где треугольники можно сделать абсолютно невидимыми для игрока.

Шестиугольные клетки могут служить имитацией трёхмерных кубов
Изометрическая проекция куба – это шестиугольник. Разделяя каждую клетку на три ромба и используя подходящее затенение, можно добиться эффекта трёхмерных кубов (если нужно, чтобы каждая «грань» куба была отдельной ячейкой, используйте ромбическую сетку – она сама построена на основе шестиугольной).
Этот факт пригодился многим играм, первой из которых была Q*bert, в своё время (1982) расхваливаемая за использование 3D.


Если вы допускаете пересечение шестиугольников, можно добиться и более впечатляющих 3D-эффектов. Такое уже использовалось в карточных играх, как на примере ниже.
Дополнительно по теме:
- Апериодический пятиугольник в статье “Pentagon Tiling Proof Solves Century-Old Math Problem“.