Это цитата сообщения REMEUR Оригинальное сообщение
УЗЛЫ КАК ФОРМООБРАЗУЮЩИЕ СТРУКТУРЫ
Что привело меня к этой работе?Вот это сообщение из дневника Таня Т
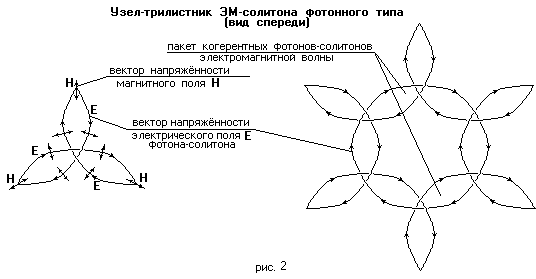
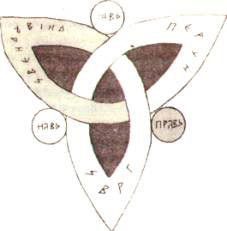
Древний славянский символ Триглав и современная схема геометрии пространства. |
|
Суббота, 18 Октября 2008 г. 10:26 + в цитатник
История теории узлов
По-видимому, К. Гаусс был первым, кто рассматривал узел как математический объект. Он считал, что анализ явлений заузливания и зацепливания является одной из основных задач «geometris situs». Сам К. Гаусс мало написал об узлах и зацеплениях, однако его ученик И. Листинг (J. Listing) посвятил узлам значительную часть своей монографии.
К концу XIX века П. Тэт (P. Tait) и К. Литл (С. Little) составили таблицы простых узлов, имеющих не более 10 пересечений, и таблицы альтернирующих простых узлов, имеющих не более 11 пересечений.
В 1906 году Г. Титце (Н. Tietze) впервые применил фундаментальную группу для доказательства нетривиальности узла. В 1927 году Дж. Александер (J. Alexander) и Л. Бриге (L. Briggs), используя коэффициенты кручения гомологии двулистных и трёхлистных разветвлённых циклических накрывающих, различили все табулированные узлы с 8 пересечениями и все узлы, за исключением трёх пар, с 9 пересечениями.
В 1928 году Александер предлагает многочлен, названный его именем, но и с его помощью не удалось убедиться в различности всех 84 узлов, имеющих не более 9 пересечений. Этот последний шаг сделал К. Рейдемейстер (К. Reidemeister), рассмотревший коэффициенты зацепления в диэдральных разветвлённых накрывающих.
Таблица узлов

Для классификации узлов составляют таблицы узлов[1] — перечень диаграмм всех простых узлов, допускающих проекции на плоскость.
Для облегчения поиска и унификации узлы имеют стандартное обозначение: первая цифра указывает число двойных точек, а вторая (расположенная в индексе) — порядковый номер узла.
Помимо стандартного обозначения несколько простейших узлов имеют специальные названия. Например:
-
узел
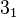 — трилистник;
— трилистник; -
узел
 — «восьмёрка», или узел Листинга;
— «восьмёрка», или узел Листинга; -
узел
 — узел «Печать Соломона».
— узел «Печать Соломона».
Для многокомпонентных узлов в верхнем индексе указывается количество компонентов: например, зацепление двух колец имеет символическую запись 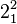 .
.
УЗЛЫ КАК ФОРМООБРАЗУЮЩИЕ СТРУКТУРЫ И ВОЗМОЖНОСТИ ИХ ПРИМЕНЕНИЯ В ДИЗАЙНЕ
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность исследования
В настоящее время исследования новых возможностей развития формообразования в дизайне всё чаще становятся междисциплинарными, объединяющими науку, технику и искусство, что является следствием поисков первичных принципов формообразования, позволяющих абстрагироваться от конкретных стилистических приёмов и методов и выйти на сущностный уровень предметно-пространственного творчества. Значительная часть авторских концепций формообразования, создававшихся с момента зарождения дизайна в начале XX в., основывалась на геометрических принципах. Отдельные математические понятия, такие как точка, линия, плоскость, объём, простейшие геометрические фигуры и их сочетания были преобразованы в первичные принципы формообразования в творчестве многих выдающихся российских (В. Кандинского, К. Малевича, В. Татлина, А. Родченко, К. Медунецкого, В. и Г. Стенбергов, К. Иогансона и др.) и зарубежных (И. Иттена, Й. Альберса, Л. Мохой-Надя, Ле Корбюзье, Б. Фуллера, К. Снельсона, Д. Эммериха, Ф. Отто и др.) дизайнеров и архитекторов, предопределившем ход развития авангардного дизайнерского и архитектурного поиска XX в.
Органичное объединение математики, искусства и дизайна наиболее успешно осуществлялось в тех областях каждой из этих сфер деятельности, где возможна визуализация и образное представление одновременно с математической формализацией и логической структурой. Такими смежными областями математики и искусства уже давно стали орнаменты, симметрия, теория пропорций, различные системы перспективы, геометрия многогранников, а в конце XX в. — также топология, фрактальная геометрия, компьютерная графика. При этом дополнительные критерии осуществимости, устанавливаемые практическим дизайном, резко снижают количество потенциально возможных заимствований принципов формообразования из области визуальной математики.
Важным источником поиска первичных принципов формообразования в дизайне является изучение истории художественного конструирования отдельных видов изделий с древнейших времён и до наших дней. Как правило, в основе традиционных приёмов формообразования также лежат геометрические принципы, которые древние мастера открывали для себя из осознанно или неосознанно поставленных экспериментов.Многие столетия, а иногда и тысячелетия, прошедшие со времени зарождения традиционных принципов формообразования, способствовали отбору наиболее эффективных и экономичных способов их практической реализации.
3
Поиск новых первичных принципов формообразования в дизайне и способов их применения в реальной предметно-пространственной и проектной деятельности возможен как внутри самой сферы дизайна, его истории и смежных с ним областях искусства, так и непосредственно в математике и естественных науках. Обнаруженные в результате инвариантные закономерности, пройдя через экспериментальную проверку триадой «материал-технология-конструкция», могут стать основой зарождения новых систем формообразования в дизайне.
Одним из фундаментальных принципов формообразования являются узлы, известные человечеству с момента зарождения самой материальной культуры, и за многие тысячелетия ставшие не только удобными и совершенными орудиями и техническими приспособлениями, но также предметом и составной частью традиционных декоративно-прикладных искусств. Узлы занимали особое место в духовной культуре многих народов, выполняя символическую и модельную роль в традиционных метафизических представлениях.
Возникшая в конце XIX — начале XX в. математическая теория узлов, уже во второй половине XX в. нашла разнообразные практические приложения в естественных науках: химии, биологии, физике, где узлы рассматриваются как форма самоорганизации в живой и неживой природе. Появились также предложения по использованию принципа узла в различных областях техники. Тема узлов стала проникать и в современное искусство: скульптуру, компьютерную графику, дизайн декоративных изделий.
В русле этих новейших тенденций поиска практических приложений теории узлов лежат исследования автора, посвящённые возможностям формообразования узлов в качестве кинематических структур изменяемых точечных поверхностей. Результаты проведённых экспериментальных и теоретических исследований позволяют говорить о появлении нового приложения теории узлов в сфере художественного формообразования, что может способствовать расширению эстетической выразительности дизайна и смежных с ним областей искусства.
^ Цель исследования — расширение возможностей художественной выразительности дизайна за счёт применения новых средств формообразования на основе геометрических структур узлов.
^ Задачи исследования:
- исследовать эволюцию практики использования узлов в материальной и ду
ховной культуре человечества;
- ввести в научный обиход явление кинематического формообразования
узлов;
- выявить основные структурные закономерности узлов и зацеплений, ока
зывающие влияние на проявление ими свойств кинематического формообразова
ния;
4
изучить основные принципы кинематического формообразования узлов;
исследовать формообразование поверхностей, получаемых трансформацией узлов из плоскости;
сравнить особенности формообразования кинематических структур узлов с известными методами формообразования на основе кинематических сетей;
- показать перспективы применения кинематических формообразующих
структур узлов в различных направлениях современного дизайна с учётом их ху
дожественно-выразительных возможностей.
^ Научная новизна. Проведено комплексное исследование эволюции узла как первичного принципа формообразования в материальной и духовной культуре человечества, предшествующей его применению в области дизайна. Обосновано новое применение узлов и зацеплений в качестве кинематических формообразующих структур. Выявлены основные принципы и закономерности формообразования узлов. Осуществлена систематизация инвариантов трансформации плоскостных форм в пространственные и соответствующих им формообразующих структур, среди которых выделены ранее неизвестные структуры изменяемой точечной поверхности, реализуемые формообразующими структурами узлов. Проведён сравнительный анализ формообразования кинематических узлов и кинематических тканевых сетей. Наглядно продемонстрированы возможности узлов как формообразующих структур для расширения образно-выразительного языка дизайна.
^ Гипотеза исследования заключается в том, что узлы, помимо своих утилитарных, декоративных и модельных функций, являются одним из первичных принципов кинетического формообразования, который может быть применён в различных областях современного дизайна.
^ Границы исследования определены кратким обзором применения узлов в материальной и духовной культуре человечества, анализом художественно-композиционных возможностей нового применения узлов в качестве формообразующих структур, математическом и физическом моделированием кинематического
5
формообразования узлов и исследованием возможностей их применимости в современном дизайне.
^ Практическая значимость работы заключается в построении действующих моделей структур изменяемой точечной поверхности, основанных на принципе узлов, в разработке унифицированного способа их построения, в выделении основных областей их возможного применения в практике современного дизайна и раскрытии их художественно-композиционных возможностей.
^ На защиту выносятся следующие результаты исследования:
новое применение узлов и зацеплений в качестве кинематических формообразующих структур;
основные принципы и закономерности кинематического формообразования узлов;
формообразование структур изменяемой точечной поверхности, реализуемых узлами и зацеплениями, в качестве нового типа объёмного формообразования из плоскости;
возможности узлов и зацеплений как кинематических структур изменяемых точечных поверхностей для расширения художественно-образного языка и формообразующих возможностей современного дизайна.
Редкие археологические находки узлов свидетельствуют о том, что в древности люди пользовались теми же узлами, которые применяются и сегодня. Древние египтяне знали беседочный узел, обнаруженный на обрывках снастей корабля фараона Хеопса, и выбленочный узел, которым была завязана верёвка, скреплявшая ручки дверей третьего помещения гробницы фараона Тутанхамона. Прямой и шкотовый узлы знали древние инки, применявшие их в конструкциях висячих мостов. Цивилизация инков изобрела также узелковое письмо, называемое «кипу». Узелковое письмо было известно и во многих других культурах. Народы Северной Европы — кельты и скандинавы — за многие столетия выработали особую культуру, в которой важную роль играли узлы.
В древних Греции и Риме широкое распространение получил прямой или геркулесовый узел, изображения которого часто встречается на осколках античной керамики. Ко временам античности относятся и первые письменные сведения об узлах. Самым известным свидетельством особой роли, которую играли некоторые узлы в древней культуре, является легенда о Гордиевом узле, сохранившаяся во многих литературных памятниках. Греческий врач Гераклес (I в. н. э.) написал сочинение о хирургических подвесках, в котором упоминает также узлы и петли.
Известный английский путешественник Дж. Смиту, в своём морском словаре, изданном в 1627 г. привёл описание некоторых морских узлов. Через сто лет узлам была посвящена подробная статья в «Энциклопедии» Дидро и Даламбера, а первая английская книга по морскому делу с рисунками узлов появилась в 1769 г. В XX в., помимо общих справочников по узлам (К. Эшли, Л. Скрягин), в которых приводится систематизация узлов по способам их практического применения, стали появляться и систематические описания декоративных узлов и плетений, включая искусство макраме и технику завязывания узлов в традиционных дальневосточных культурах.
В § 1.2 «^ Декоративные узлы и плетёный орнамент» узлы рассматриваются как элементы декоративных плетений и их изображений, известных под общим названием «плетёный орнамент».
Для изготовления плетёных изделий были необходимы узлы с регулярной структурой, что способствовало возникновению интереса к симметрии узлов. Плоские плетения приводили к основным принципам построения геометрических орнаментов, выделялись узлы, обладающие периодической структурой, комбинаторные сочетания которых могли регулярным образом заполнять плоскость.
Плетёные орнаменты и узлы обычно изготовлялись из материалов растительного и животного происхождения и были недолговечны. Возможно, что это стало стимулом для поиска других форм их художественного представления, таких как графические изображения, резьба, чеканка, литье, и т. п., что привело к воз-
8
никновению плетёного орнамента, известного практически во всех человеческих культурах уже с глубокой древности. Среди разнообразных форм плетёного орнамента широкое распространение получили структуры, выполненные из непрерывной линии, начало и конец которой соединены между собой. К ним относятся, в частности, многие кельтские узлы, тамильские орнаменты, рисунки африканского народа Чокве и др.
Плетёным орнаментом из непрерывных линий, образующих структуры узлов, занимались и всемирно известные художники эпохи Возрождения: Леонардо да Винчи и Альбрехт Дюрер. В росписи Геральдической залы дворца Сфорца в Милане Леонардо изобразил ветви деревьев, переплетенные декоративным шнуром, образующим сложные узлы и петли. Единственным орнаментальным мотивом портрета Джоконды является расположенный на краю выреза её платья узор из переходящих друг в друга четырёхлепестковых узлов, последовательно завязанных друг за другом на непрерывном шнуре. Леонардо создал также рисунок центрической орнаментальной композиции из непрерывного переплетенного шнура, образующего множество переходящих друг в друга узлов, вдохновивший Дюрера на создание серии аналогичных гравюр на дереве, которые он сам называл «Узлы».
Исследователи плетёного орнамента выделяют всего четыре основных узла, а остальные рассматривает как их производные, которые получаются за счет усложнения этих четырёх. К этим узлам относятся прямой или геркулесов узел, «вечный» узел, узел «древо жизни», а также «плоский» или «турецкий» узел.
Первые попытки дать узлам математическое описание также были связаны с плетёными орнаментами. В статье А. Т. Вандермонда 1771 г., считающейся первой публикацией по теории узлов, приводится рисунок системы зацепленных петель, напоминающих плетёную ткань. Другой основоположник теории узлов, К. Гаусс, также проявлял интерес к закономерным структурам плетёных орнаментов, модулями которых являются симметричные узлы и зацепления.
В § 1.3 «^ Символика узлов и её отражение в традиционном мировоззрении» исследуются свидетельства того, что узлы занимали особое место в традиционной духовной культуре многих народов, выполняя роль символических и модельных объектов, применявшихся для описания космологических и метафизических представлений, ставших прообразами современных математических моделей.
В 1924 г. П. Флоренский в своих исследованиях по теории искусства, прочитанных им на полиграфическом факультете ВХУТЕМАСа, ставил под сомнение и исключительно технологическую природу происхождения орнамента. Флоренский трактовал изобразительность орнамента как символическое отображение метафизических явлений и процессов, как особый язык символистической философии, на котором только и могут быть переданы сокровенные принципы строения мироздания.
9
Народы самых разных культур использовали символический язык узлов. Например, сплетенные узлами стебли тростника и полоски коры, символизировали заключение мира между двумя племенами Новой Каледонии. Эскимосы рассказывают свои сказания, делая узлы на нескольких параллельных веревках, изображающих сцены охоты и различных животных. Подобный же приём рассказывания древних мифов с помощью веревочных фигур применяют и жители острова Пасхи. Островитяне Тихого океана используют своеобразный вид узелкового письма, изготавливая сплетенные из пальмовых листьев и волокон пандануса карты океанских течений и господствующих ветров, вплетая в них раковины каури, изображающие острова и рифы.
В Прибалтике узелковое письмо из разноцветных нитей и узелков представляло собой средство выражения особых чувств и пожеланий при их дарении — почтения, уважения, любви. Японские ритуальные узлы мицухики составляют часть традиционного японского этикета в преподношении подарков. Они изготавливаются из спрессованных бумажных шнуров, имеют чёткую последовательность процесса завязывания, составляющего сам ритуал, и содержат в себе символическое значение.
Верёвка с двенадцатью завязанными на ней через равные промежутки узлами использовалась древними строителями как инструмент для разметки на местности прямых углов, натягивая которую, они образовывали Египетский или Священный треугольник со сторонами, относящимися друг к другу как 3, 4 и 5. Верёвка с последовательно завязанными на ней узлами-восьмёрками постепенно приобрела символическое значение как один из атрибутов строительного искусства и часто изображалась в качестве символа так называемой «цепи единства», окружающей помещение масонских лож в их верхней части. Согласно Р. Генону, традиционно всякое здание строилось согласно космической модели, и ложа как образ Космоса должна была иметь обрамление в виде шнура с двенадцатью узлами, также как и сам Космос ограничен кругом из двенадцати созвездий Зодиака.
Традиционное мировоззрение видит в замкнутой непрерывной нити не только средство ограничения и упорядочивания разнообразных элементов, составляющих Космос, но и связь всех элементов между собой, в чём и проявляется её функция «цепи единства». Генон, исследуя символику плетёных орнаментов, в которых фигуры изображаются непрерывной линией, в частности работ Леонардо и Дюрера, отмечал, что непрерывный характер линии сближает их по своей форме с лабиринтами.
Орнамент-лабиринт из непрерывной нити или его стилизованное изображение в виде геометрических фигур, параллельно со своим символическим значением сакрального обрамления, несущего космогонический смысл, имел и ряд вспомогательных производных функций, таких как защитные, охранительные и магические. Постепенное вырождение понимания всей глубины изначальной
10
Традиции сводило и смысл орнамента только к этим вторичным функциям, выводя на первое место магическое значение.
Магические и колдовские свойства с глубокой древности приписывались узлам и кольцам самыми различными народами, когда свойства узлов, понимаемые как нечто связывающее, стягивающее и запутывающее, то есть налагающее узы на объект магического воздействия, переносились на внешние предметы и людей физически с магическими узлами не соприкасающимися, но находящимися с ними в симпатической связи.
В § 1.4 «^ Зарождение и развитие теории узлов» рассматриваются основные этапы процесса становления научного представления об узлах.
Изучение узлов и зацеплений стало одним из разделов топологии, который тесно связан с алгеброй, геометрией, теорией групп, теорией матриц, теорией чисел и другими областями математики. С точки зрения топологии, узел — это одномерная кривая, расположенная в обычном трехмерном пространстве так, что она начинается и заканчивается в одной и той же точке и не пересекает саму себя. Два и более узла могут образовывать зацепления — связные структуры, которые невозможно разделить без разрывов составляющих их узлов.
Возникновение математической теории узлов положила начало статья А. Т. Вандермонда «Заметки по вопросам расположений» (1771), интерес к узлам проявлял и К. Ф. Гаусс. Ученик Гаусса И. Б. Листинг в своей монографии «Предварительные исследования по топологии» (1847) впервые сформулировал постановку задачи о расположении в пространстве замкнутой кривой линии, то есть проблему узлов.
Возникновение современной теории узлов связано с именами Г. Гельмгольца, У. Томсона (лорд Кельвин), Дж. К. Максвелла и П. Тейта. Концепция вихревых атомов, которую в середине XIX в. выдвинул У. Томпсон, предполагала идентичность узлов и атомов различной формы, образованных замкнутыми и заузленны-ми вихрями эфира. Тейт в сотрудничестве с Т. Киркманом и Ч. Литтлом уже к 1900 г. классифицировал простые узлы до десяти скрещений, а первый полный перечень всех простых узлов с девятью и менее скрещениями, был опубликован в 1932 г. немецким математиком К. Рейдемейстером. Перечень диаграмм простых узлов до восьми скрещений приведен на рисунке 1. Каждая диаграмма снабжена индексом, состоящим из двух чисел: первое число обозначает количество скрещений данного узла, а второе — его порядковый номер среди узлов, содержащих одинаковое количество скрещений.
Современный математический аппарат позволяет записывать любой узел в виде его полинома и проводить поиск и классификацию неразложимых узлов и зацеплений с помощью компьютеров, однако для выявления эстетических свойств узлов их графическое изображение и моделирование приобретают важное значение.
11
В § 1.5 «^ Узлы в современном искусстве и дизайне» рассматривается проникновение темы узлов в современное искусство и её авторское прочтение художниками и дизайнерами.
Рост научного интереса к узлам как объектам абстрактно-математической природы в конце XIX — начале XX в. породил и эстетический интерес к ним. По-видимому, первым современным художником, обратившимся к теме узлов, был А Флокон, выпускник Баухауза, чьи работы оказали большое влияние на творчество М. Эшера. Флокон писал об узлах, рисовал их и делал их бумажные модели узлов. М. Эшер также строил модели узлов, ставшие прообразами узлов на его гравюрах. Флокон и Эшер изображают узлы с соединёнными концами — то есть как топологические узлы, несущими в себе современную эстетику искривлённой, подвергнутой воздействию внешних сил пространственной формы. Художники предлагают зрителю любоваться сложной и непривычной формой, по-разному открывающейся с различных ракурсов.
Б. Фуллер в своём труде «Синергетика» (1982), посвятил несколько страниц формообразующему принципу узла. Фуллер отделяет узел как формообразующий принцип от его материальных проявлений, таких как физические свойства верёвки, её цвет, текстура, рассматривая свободно перемещающийся вдоль верёвки узел как структурный принцип интеллектуального порядка. Минимальный узел трилистник, образованный из двух окружностей, Фуллер трактует как элементарный пространственный модуль, соотнося его с основным модулем синергетических структур — тетраэдром. Тем самым Фуллер включил узлы в свою концепцию си-нергетического формообразования, подразумевая в них потенциальные формообразующие возможности аналогичные его сжато-растянутым стержне-вантовым структурам.
Современные художники, скульпторы и дизайнеры (Дж. Робинсон, Г. Джонс Н. Фридман, С. Яблан) обращаются к узлам как к эффективному средству выразительности, формы которых порождают образность и экспрессию восприятия замкнутой линии в пространстве.
В Главе 2 «Узлы в качестве формообразующих структур» рассматривается новое применение узлов и зацеплений в качестве кинематических формообразующих структур и основные принципы и закономерности их формообразования.
В § 2.1 «^ Узлы как волновые кинематические формообразующие структуры» рассматривается сущность нового применение узлов в качестве формообразующих структур. Завязывание узлов как принцип формообразования встречается уже в живой природе, где оно выполняет функции пространственной самоорганизации молекул, в частности ДНК, отдельных микробов и некоторых многоклеточных организмов.
Утилитарные затягиваемые узлы действуют как волновые процессы, на этом
12
принципе основаны разнообразные бегущие и скользящие узлы, перемещающиеся как единое целое по верёвке, не меняя своей формы. За счёт трения верёвки в точках её скрещений перераспределение верёвки внутри узла становится неравномерным, в результате чего узел уменьшается в размерах и в конце концов затягивается.
Узел может быть завязан также и на длинномерном объекте, обладающим внутренней упругостью, например на резиновом стержне или стальной проволоке. В этом случае узел будет стремиться уравновесить действие сил трения, стремящихся уменьшить его размеры, и сил упругости, сопротивляющихся этому, что и определяет итоговую форму узла.
В узлах из упругого одномерно протяжённого материала существуют два типа волн: горизонтальные, расположенные параллельно плоскости проекции и образованные их замкнутыми витками, и вертикальные, образованные переплетёнными скрещениями узла. Первый тип волн сохраняет при движении свою форму подобно солитонам — объектам, сочетающим свойства волн и частиц и играющих важную роль в современных нелинейных теориях естествознания, а второй представляет собой бегущие поперечным волнам деформации на протяжённых деформируемых телах. В затягиваемых узлах бегущие поперечные волны деформации определяют характер их затягивания, поэтому такую важность приобретает порядок переплетения в узле, тогда как форма витков играет вторичную роль. Напротив, в декоративных узлах и плетениях главную роль играют витки и их форма, а переплетения призваны обеспечивать сохранение формы витков.
Витки-солитоны могут быть образованы на замкнутом упругом одномерно протяжённом объекте топологически эквивалентном кольцу или тривиальному узлу. Простейший узел трилистник при этом может быть образован как зацепление единственного витка-солитона за свободную часть кольца.
Трилистник является торическим узлом, то есть обмоткой поверхности тора — двумерного многообразия с одной дыркой. Некоторые другие узлы могут также быть расположены на соответствующих двумерных многообразиях: кольцо, или тривиальный узел, располагается в виде обмотки на сфере, а узел восьмёрка — на кренделе с двумя дырками. Трилистник может быть представлен в виде двух зеркальных обличий — левого и правого, топологически не преобразуемых друг в друга, каждый из которых может быть завязан на поверхности тора без контактирующих точек скрещений, но будучи завязанными вместе на одном и том же торе, они физически контактируют друг с другом в общих точках скрещений, образуя структуру заузленной ткани на поверхности тора, представляющей собой модель точечной поверхности тора. Аналогичным образом можно построить модель точечной поверхности произвольного ориентируемого двумерного многообразия, располагая на его поверхности по меньшей мере два зеркальных узла-обмотки соответствующего типа.
13
Энергии упругости в заузленном стержне, зависящая от топологической сложности узла, стремясь принять наименьшее значение, приводит к тому, что его средняя линия стремится совпасть с плоскостью, в результате чего все скрещения узла становятся реально контактирующими, и их множество формирует точечную модель плоскости. При этом плоская модель точечной поверхности, заданная узлом или зацеплением нескольких узлов, в результате приложения к ней внешнего усилия и создания избыточной внутренней энергии упругости, может быть выведена из плоскости и преобразована в пространственное положение. Такие заузленные структуры, моделирующие точечные поверхностей и действующие как волновые механизмы, автор предложил называть специальным термином «NODUS структуры» (от лат. nodus, — узел).
В § 2.2. «^ Анализ свойств симметрии и модулярности циклических узлов и зацеплений» исследуется типы узлов и зацеплений, которые потенциально могут моделировать кинематические точечные поверхности, способные совмещаться с плоскостью и образовывать пространственные поверхности-оболочки.
Любой узел или зацепление с некоторым количеством контактирующих скрещений, моделирует фрагмент точечной поверхности, но её обратимую кинематическую изменяемость происходящую вследствие трансформации, а не деформации структуры, могут обеспечить только те из них, которые обладают циклической упорядоченностью. Регулярность узлов и зацеплений, придающая им формообразующие свойства, проявляется в циклическом заполнении их образующими кольцевой области между двумя замкнутыми огибающими.
Анализ симметрии диаграмм неразложимых узлов и зацеплений из таблиц Д. Рольфсена (1976) показывает, что преобладающим видом симметрии для них является осевая симметрия порядка n, где n — любое число от 1 до ∞. Такая симметрия в основном характерна для орнаментов и возникает благодаря применению принципа переплетения, который приводит к выпадению плоскостей симметрии, пересекающихся по оси симметрии. Для узлов и зацеплений наибольший из возможных порядков оси симметрии может рассматриваться как инвариант. Так, например, трилистник можно представить на плоскости в виде двух топологически равноправных обличий диаграмм, одно из которых имеет порядок оси симметрии равный двум, а другое — трём. Диаграмма трилистника с большим значением порядка оси симметрии может быть отнесена к циклическому (периодическому) типу узлов моделирующим своей структурой изменяемые точечные поверхности.
В результате проведённого анализа установлено, что для циклических узлов и зацеплений принадлежность к симметричным или асимметричным структурам определяется исключительно положением их образующих относительно точечной поверхности, а не взаимным расположением задающих её точечных контактов. Следствием этого стал принятый автором дифференцированный подход к симме-
14
трии собственно узлов и зацеплений и симметрии задаваемых ими точечных систем, для чего циклические узлы и зацепления были представлены в виде универсальных диаграмм, расположенных на срединной точечной поверхности, моделируемых плоскими кривыми и являющихся графами с вероятностным взаимным положением пересекающихся участков кривых в каждой вершине. Универсальные диаграммы содержат в себе 2n потенциально возможных узлов или зацеплений где n — количество точек скрещений или вершин данной плоской диаграммы.
В § 2.3 «^ Принципы развития циклических узлов и зацеплений в NODUS структуры» рассматривается задача закономерного перехода от простейших узлов и зацеплений, представленных в математических перечнях, к NODUS структурам с гораздо большим числом двойных точек, достаточным для возникновения у них точечной поверхности и проявления ими формообразующих свойств.
Эксперименты, проведенные автором, показали, что минимальное количество контактирующих скрещений у циклического узла или зацепления, необходимое для проявления ими кинематических свойств обратимой трансформации должно быть не менее двух-трёх десятков. Помимо количественных критериев, большое значение имеет и качественные, то есть порядок распределения множества контактирующих скрещений по структуре узла или зацепления.
Получение сложных узлов на основе простейших известно как «развитие узлов» и широко применяется в построении плетёных орнаментов, в частности кельтских, однако при орнаментальном развитии каждый производный узел имеет связь только с исходным узлом, а какая-либо связь между отдельными производными узлами отсутствует.