Максимилье́н Мари́ Изидо́р де Робеспье́р (фр. Maximilien Marie Isidore de Robespierre; 6 мая 1758[1][2][…], Аррас — 28 июля 1794[1][2][…], Париж) — французский революционер, адвокат, один из наиболее известных и влиятельных политических деятелей Великой французской революции.Избранный депутатом от третьего сословия в Генеральные штаты в 1789 году, он вскоре стал одним из ведущих деятелей демократов в Учредительном собрании, выступая за отмену рабства, смертной казни, а также за всеобщее избирательное право. Его последовательность в отстаивании своих принципов вскоре заслужила ему прозвище «Неподкупный» (фр. L’Incorruptible)[пр 1]. Член Якобинского клуба с момента его основания, он являлся самым известным и ведущим его членом. Противник войны с Австрией в 1792 году. Поддержал падение монархии и провозглашение республики. Член повстанческой Парижской коммуны, был избран в Национальное собрание (Конвент), где находился на скамьях Горы и выступал против политики жирондистов[пр 2]. После восстания 31 мая — 2 июня 1793 года стал членом Комитета общественного спасения 27 июля 1793 года, участвовал в создании революционного правительства в контексте войны против коалиции иностранных монархий и гражданской войны. Выступал за политику дехристианизации и, после победы комитетов общественного спасения и общественной безопасности над фракциями эбертистов и дантонистов, весной 1794 года провозгласил культ «Верховного Существа» и поддержал принятие закона от 22 прериаля (10 июня 1794 года), ознаменовавшего собою начало периода «большого террора». Изолированный в Комитете общественного спасения и атакованный в Конвенте бывшими эбертистами слева и дантонистами справа, выступает перед Конвентом 8 термидора II года (26 июля 1794 года). На следующий день, 9 термидора II года (27 июля 1794 года) после бурного заседания в Конвенте он был арестован вместе со своим братом Огюстеном и соратниками Кутоном, Сен-Жюстом и Леба. После восстания Парижской коммуны того же дня в поддержку арестованных объявлен Конвентом вне закона и казнён без суда и следствия на следующий день, 10 термидора (28 июля 1794 года) с 21 своим сторонником.

А́льбрехт Дю́рер (нем. Albrecht Dürer, немецкое произношение: [ˈʔalbʁɛçt ˈdyːʁɐ][1][2][3]; 21 мая 1471, Нюрнберг — 6 апреля 1528, Нюрнберг) — немецкий живописец, рисовальщик и гравёр, один из величайших художников Северного Возрождения[4]. Признан крупнейшим европейским мастером ксилографии[5][6], поднявшим её на уровень настоящего искусства[7]. Первый теоретик искусства среди североевропейских художников[8][9], автор практического руководства по изобразительному и декоративно-прикладному искусству на немецком языке, пропагандировавший необходимость разностороннего развития художников. Основоположник сравнительной антропометрии в качестве раздела теории пропорционирования в искусстве. Помимо перечисленного оставил заметный след в военно-инженерном деле разработкой теории фортификации[10]. Первый из европейских художников, написавший автобиографию. Гравюры Альбрехта Дюрера широко представлены в музейных и частных собраниях[11].

Ксенофо́бия (от греч. ξένος «чужой» + φόβος «страх») — нетерпимость к кому-либо или чему-либо чужому, незнакомому, непривычному^[3]; восприятие чужого как неприятного и опасного. Ведёт к исключению из местного сообщества категорий лиц, которые рассматриваются как «чужие», их дискриминации в политике, быту, сфере занятости, образования и социального обеспечения.

В медицинской сфере ксенофобия в качестве боязни чужого, незнакомого рассматривается как разновидность навязчивых состояний^[3].

Сосна болотная[1], или длиннохвойная (лат. Pínus palústris) — североамериканский вид растений рода Сосна (Pinus) семейства Сосновые (Pinaceae). Является деревом-символом штата Алабама.Мужские стробилы. Сосна болотная — дерево до 47 м в высоту, ствол которого достигает 1,2 м в диаметре, с округлой кроной. Кора рыже-коричневая, чешуйчато-бороздчатая. Молодые ветки оранжево-бурые, затем темнеющие. Почки серебристо-белые, яйцевидные, до 4 см. Хвоя сохраняющаяся на протяжении 2 лет. Хвоинки собранные в пучки обычно по 3, реже по 2, длинные, до 45 см длиной, прямые, различных оттенков жёлто-зелёного цвета; края хвоинок мелкозубчатые. Мужские стробилы цилиндрической формы, около 5 см длиной, сиреневатого цвета. Женские стробилы двулетние, незрелые — ланцетовидные, затем раскрывающиеся и становящиеся узко-яйцевидными, тёмно-коричневого цвета, 15—25 см длиной. Чешуйки жёсткие, с коротко-заострённой верхушкой. Семена притупленно-обратнояйцевидной формы, около 10 мм, светло-коричневые, с крылом до 4 см.

Росто́вский кре́мль — первоначально резиденция митрополита Ростовской епархии, называвшаяся митрополичьим (архиерейским) двором. Расположен в центре Ростова Великого около озера Неро. В настоящее время ансамбль кремля состоит из архиерейского двора, примыкающей к нему с севера Соборной площади с Успенским собором и с юга — митрополичьего сада[1].Во время постройки Ростов уже не имел какого-либо оборонного значения, в связи с чем оборонительные сооружения кремля имеют некоторые архитектурные упрощения, которые пришлось бы устранять в случае военной опасности — широкие въездные ворота, отсутствие подошвенных бойниц в башнях, линию верхнего боя в башнях продолжают окна с наличниками и другие. Тем не менее, кремль построен в традициях русского оборонного строительства более раннего периода и является памятником русской военной архитектуры допетровского времени.С 1998 года Ростовский кремль входит в предварительный список Всемирного наследия ЮНЕСКО[2].

 

Романтизм в русской литературе — литературное течение, господствовавшее в России преимущественно в первой половине XIX века (примерно с 1790-х по 1840-е годы), отражавшее глубокие социально-политические и духовные изменения в стране. Он представлял собой специфическую русскую модификацию общеевропейского романтизма, нашедшую яркое выражение в литературе, музыке и живописи. В отличие от западноевропейского романтизма, который часто противопоставлял себя Просвещению, русский романтизм в значительной степени развивался на его почве, синтезируя просветительские идеи с новыми эмоциональными и мистическими настроениями.

 

Симплокарпус зловонный (лат. *Symplocarpus foetidus*) — вид многолетних травянистых растений из семейства ароидных (Araceae). Это растение известно своим характерным запахом и необычной формой цветков.❇️ Ботаническое описание

Симплокарпус зловонный — это травянистое растение, достигающее высоты от 15 до 30 см. Оно имеет крупные, сердцевидные листья, которые появляются после цветения. Листья могут достигать 30 см в ширину и 50 см в длину, они имеют гладкую поверхность и ярко-зеленый цвет. Цветение происходит ранней весной, обычно в марте или апреле, когда листья еще не распустились. Цветок представляет собой соцветие, называемое «початком», окруженное крупным, мясистым, обычно пурпурным или зеленым покрывалом (спадом). Это покрывало имеет форму колокола и служит для привлечения опылителей, таких как мухи. Симплокарпус зловонный получил свое название из-за характерного неприятного запаха, который выделяется во время цветения. Запах напоминает гниющее мясо и служит для привлечения насекомых-опылителей, которые ищут источники пищи.

 

Уличить (от глагола «уличать») — в русском языке глагол, означающий разоблачить, доказать виновность кого-либо в чём-либо. Это переходный глагол, требующий прямого дополнения (кого? в чём?). Семантика: Глагол «уличить» подразумевает не просто доказательство факта, но и раскрытие и демонстрацию вины, часто с оттенком обвинения и осуждения. В отличие от простого «доказать», «уличить» включает в себя элемент неожиданности, разоблачения или неожиданного обнаружения истины. Возможны эмоциональные оттенки, от гневного разоблачения до спокойной констатации факта.

 

Рели́кт (лат. relictum — «остаток») — вид (или другой таксон) живых организмов, сохранившийся в данном регионе от флоры или фауны прошлых геологических эпох и находящийся в некотором несоответствии с современными условиями существования^[1]. Реликты являются проявлением прошлого в наше время^[2]. К реликтам относятся все палеоэндемики^[3]. Термин реликт ввёл в научный оборот немецкий географ и антрополог Оскар Пешель в 1875 году^[4].

 

Прикладна́я му́зыка — музыка, которая функционирует не как самодостаточная сущность, но выполняет какие-либо утилитарные общественные функции: сопровождение церемоний и культов, военных маршей и светских танцев, развлечение, терапия и т.д. Термин «прикладная музыка» (нем. angewandte Musik) противопоставляется термину «чистая музыка» (нем. reine Musik).

 

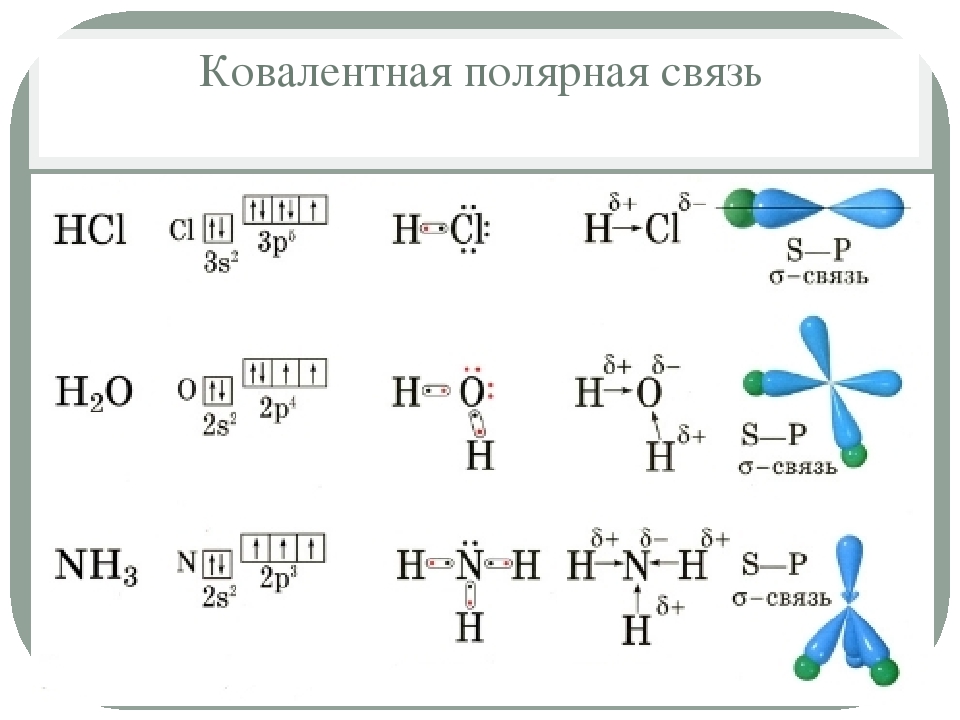
Дистрибути́вность (от лат. distributivus «распределительный»), также распределительный закон^[1] — свойство согласованности двух бинарных операций, определённых на одном и том же множестве.

Говорят, что бинарная операция «×» является дистрибутивной относительно бинарной операции «+»^[2], если они удовлетворяют следующим двум тождествам:

${\displaystyle (\mathrm{\forall }x,y,z)x\times (y+z)=(x\times y)+(x\times z)}$ — дистрибутивность слева;

${\displaystyle (\mathrm{\forall }x,y,z)(y+z)\times x=(y\times x)+(z\times x)}$ — дистрибутивность справа.

Если операция «×» является коммутативной, то свойства дистрибутивности слева и справа равносильны.

Относительно соответствующих аддитивных операций, мультипликативные операции в кольцах и полях, по определению, удовлетворяют свойству дистрибутивности.

Если операции сложения и пересечения для односторонних идеалов некоторого кольца (или подмодулей некоторого модуля) удовлетворяют свойству дистрибутивности^{[уточнить]}, то говорят о дистрибутивном кольце (или дистрибутивном модуле).

 

Квота (от лат. quot — сколько) — доля, часть, норма чего-либо допускаемого. Например, импортная квота, избирательная квота (количество голосов, необходимое каждому кандидату для избрания при пропорциональной системе выборов), налоговая квота (размер налога, устанавливаемый с каждой единицы обложения).

 

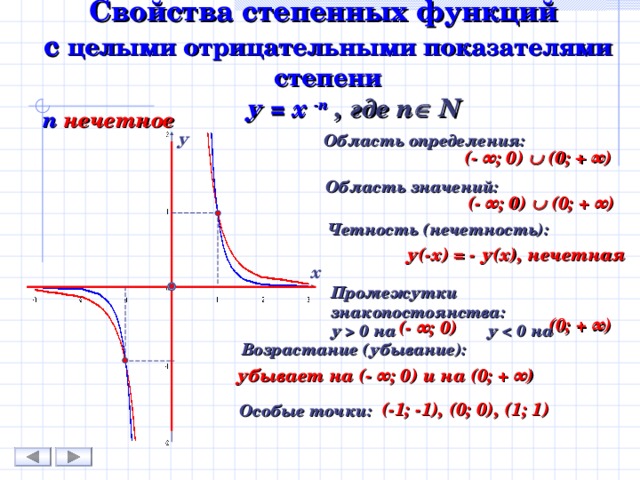
Степенная функция — это функция вида ( f(x) = a cdot x^n ), где ( a ) — коэффициент, ( n ) — степень (целое или дробное число), а ( x ) — переменная. Степенные функции являются важным классом функций в математике и широко используются в различных областях науки и техники.

Метафизи́ческая живопи́сь (итал. pittura metafisica), направление, сложившееся в итальянском изобразительном искусстве 1910-х гг. Противопоставила футуризму, технократически устремленному в будущее, принципы поэтической созерцательности и покоя, идею возврата к «классическим ценностям». Основоположники направления (Дж. де Кирико и К. Карра) сочетали в своих полотнах классические — античные и ренессансные — мотивы с настроениями ирреальности, где «метафизические» вещи заменили человека. Став одним из преддверий сюрреализма, метафизическая живопись развивалась и как самостоятельная тенденция, близкая магическому реализму.

Рецензирование (англ. peer review) — процедура рассмотрения научных статей и монографий учёными-специалистами в той же области (отсюда название в некоторых языках — «рассмотрение коллегами», «равными»: англ. peer review, исп. revisión por pares). Цель рецензирования до публикации — убедиться в точности и достоверности изложения и в необходимых случаях добиться от автора следования стандартам, принятым в конкретной области или науке в целом. Публикации произведений, не прошедших рецензирования, часто воспринимаются с недоверием профессионалами во многих областях науки и искусства.

Облихование- в русском государстве XVi-XVII вв. особая форма судебного процесса, впервые предусмотренная судебником 1550 г.: когда подозреваемого обвиняли в том, что он ведомо лихой человек, этого было достаточно для применения к нему пытки. если после этого он сознавался в преступлениях, его предавали смертной казни. к лихим, т.е. самым опасным делам, относились разбой, грабеж, поджог, убийство, особые виды татьбы.

 

Гарантия — это обязательство, которое берет на себя производитель или продавец товара, либо исполнителя услуги, по обеспечению определенных условий качества, сроков и функциональности продукта или услуги. Гарантия служит защитой интересов потребителя и подтверждает, что товар или услуга будут работать в соответствии с заявленными характеристиками в течение определенного времени.

 

Cагитта́льный (от лат. sagitta — стрела)  анат. делящий (тело) продольно на правую и левую половину (о линии, плоскости, разрезе) ◆ При описании частей тела и положения отдельных органов используют три взаимно перпендикулярные плоскости: сагиттальную, фронтальную и горизонтальную. Сагиттальная плоскость проходит в переднезаднем направлении и делит тело человека на правую (dexter) и левую (sinister) части. Сагиттальная плоскость, проходящая через середину тела, называется срединной, или медианной. Рудольф Самусев, Юрий Селин, "Анатомия"

 

 

 

Сложноподчинённое предложение (СПП) — это сложное предложение, части которого связаны подчинительной связью, то есть одна часть (придаточное предложение) зависит от другой (главного предложения) и не может существовать самостоятельно как отдельное предложение. Главное предложение семантически и грамматически доминирует над придаточным. В отличие от сложносочинённых предложений, части СПП не равноправны. Сложноподчинённые предложения — одна из самых распространённых конструкций в русском языке, позволяющих выразить сложные смысловые отношения между событиями, явлениями и фактами. Анализ таких предложений требует понимания роли каждого придаточного и его связи с главным предложением.

Этимоло́гия (др.-греч. ἐτυμολογία от ἔτυμον — истина, основное значение слова и λόγος — слово, учение, суждение) — термин, означающий:

• раздел лингвистики (сравнительно-исторического языкознания), изучающий происхождение слов (устойчивых оборотов^[1] и реже морфем)^[2];
• методику исследований, используемых при выявлении истории происхождения слова (или морфемы);
• результат такого выявления^[3];
• под этимологией может также пониматься любая гипотеза о происхождении того или иного конкретного слова^[1] или морфемы (например, «предложить более убедительную этимологию»), само происхождение слова (например, «у слова тетрадь греческая этимология»), то есть версию происхождения — непосредственно этимон.

Термин «этимология» зародился в среде древнегреческих философов-стоиков и, согласно поздним свидетельствам Диогена Лаэртского, приписывается Хрисиппу (281/278—208/205 до н. э.). До XIX века термин «этимология» в языкознании мог применяться в значении «грамматика»^[4]. Первоначально, у древних — учение об «истинном» («первоначальном») значении слова: см. Исидор Севильский (ок. 560—636) — энциклопедия «Этимологии».

Редукция (от лат. *reductio* — возвращение, приведение) — многозначный термин, используемый в различных областях науки и техники. Общее значение сводится к уменьшению, упрощению, приведению к более простому виду или состоянию. В зависимости от контекста.

Подобие в геометрии — это отношение между двумя геометрическими фигурами, при котором одна фигура является уменьшенной или увеличенной копией другой, сохраняя при этом форму и пропорции. Более формально, две фигуры подобны, если существует соответствие между их точками такое, что отношение расстояний между любыми двумя точками одной фигуры и соответствующими им точками другой фигуры постоянно. Это постоянное отношение называется коэффициентом подобия (или коэффициентом масштабирования).

Хорезмийцы (др.-греч. Ηαρaςμιάη, перс. خوارزمىان‎, туркм. Horezmliler, узб. Xorazmiylar) — исторический народ иранского происхождения^[1][2], составлявшие ядро населения древнего Хорезма (Khwārezm), непрерывное присутствие которых в Центральной Азии засвидетельствовано с середины первого тысячелетия до н. э. Входили в союз сако-массагетских племён^[3]. Также древние хорезмийцы были одним из компонентов в формировании узбеков и туркмен^[4][5][6][7].

вверх^ к полной версии понравилось! в evernote

Вы сейчас не можете прокомментировать это сообщение.

Дневник Ксенофо́бия | percepnef - О мире, о религии, о времени, о советской стране и о себе | Лента друзей percepnef / Полная версия Добавить в друзья Страницы: раньше»