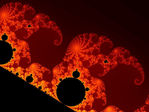
Фракта́л (лат. fractus — дроблёный, сломанный, разбитый) — сложная геометрическая фигура, обладающая свойством самоподобия, то есть составленная из нескольких частей, каждая из которых подобна всей фигуре целиком.
Фрактал — самоподобное множество нецелой размерности.
Фрактал — это бесконечно самоподобная геометрическая фигура, каждый фрагмент которой повторяется при уменьшении масштаба.
какие фракталы окружают Вас? жду фотографий
Термин
Следует отметить, что слово «фрактал» не является математическим термином и не имеет общепринятого строгого математического определения. Оно может употребляться, когда рассматриваемая фигура обладает какими-либо из перечисленных ниже свойств:
- Обладает нетривиальной структурой на всех масштабах. В этом отличие от регулярных фигур (таких, как окружность, эллипс, график гладкой функции): если мы рассмотрим небольшой фрагмент регулярной фигуры в очень крупном масштабе, он будет похож на фрагмент прямой. Для фрактала увеличение масштаба не ведёт к упрощению структуры, на всех шкалах мы увидим одинаково сложную картину.
- Является самоподобной или приближённо самоподобной.
- Обладает дробной метрической размерностью или метрической размерностью, превосходящей топологическую.
Многие объекты в природе обладают фрактальными свойствами, например, побережья, облака, кроны деревьев, снежинки, кровеносная система и система альвеол человека или животных.
Фракталы, особенно на плоскости, популярны благодаря сочетанию красоты с простотой построения при помощи компьютера.
Множество Мандельброта — классический образец фрактала
История
Первые примеры самоподобных множеств с необычными свойствами появились в XIX веке (например, множество Кантора). Термин «фрактал» был введён Бенуа Мандельбротом в 1975 годуи получил широкую популярность с выходом в 1977 году его книги «Фрактальная геометрия природы».
Фрактальная форма подвида цветной капусты (Brassica cauliflora)
Рекурсивная процедура получения фрактальных кривых
Существует простая рекурсивная процедура получения фрактальных кривых на плоскости. Зададим произвольную ломаную с конечным числом звеньев, называемую генератором. Далее, заменим в ней каждый отрезок генератором (точнее, ломаной, подобной генератору). В получившейся ломаной вновь заменим каждый отрезок генератором. Продолжая до бесконечности, в пределе получим фрактальную кривую. На рисунке справа приведены три первых шага этой процедуры для кривой Коха.
Примерами таких кривых служат:
- кривая дракона;
- кривая Коха;
- кривая Леви;
- кривая Минковского;
- кривая Пеано.
- с помощью похожей процедуры получается дерево Пифагора.
Лес, Волны, Снежинка, Кожа...